HiPPO (2020) 논문 리뷰

Time Series

HiPPO (2020) 논문 리뷰

아르카눔 2025. 5. 17. 00:29

HiPPO 논문의 이름은 HiPPO: Recurrent Memory with Optimal Polynomial Projections다. (링크)

저자는 Albert Gu, Tri Dao, Stefano Ermon, Atri Rudra, Christopher Re다.

HiPPO는 시계열 데이터 혹은 sequential data에서 순서에 따라서 정보를 누적하는 문제를 풀고자 하는 논문이다.

전 직장에서 동료들의 도움으로 읽었던 논문인데 다시 한 번 정리한 리뷰다.

저자들이 물리학 베이스인 것으로 알고 있어서 수식이 난무한다.

Abstract:

Sequential data 순차적 데이터 학습의 핵심 문제는 더 많은 데이터를 처리함에 따른 cumulative history 누적된 과거 기록을 incremental fashion 점진적인 방식의 표현이다. 저자들은 continuous signals 연속적인 신호 혹은 discrete time series 이산적인 시계열의 online compression에 대한 일반적인 프레임 워크인 HiPPO를 제안하는데 히포는 polynomial basis로의 projection에 기반한다. 과거의 매 time step 마다의 중요성을 측정하는 measure 측도가 주어질 때 HiPPO는 online function approximation problem에 대한 자연스러운 optimal solution 최적의 해를 제공한다. 특별한 경우로서, HiPPO 최근의 Legendre Memory Unit (LMU)을 first principles 제1원리 로부터 짧은 유도로 부터 도출하며, GRU와 같은 순환 신경망의 보편적인 gating 메커니즘을 일반화한다. 시간 스케일에 대한 사전 정보 없이 모든 과거를 기억하기 위해 시간적으로 확장되는 새로운 메모리 업데이트 메커니즘(HiPPO-LegS)을 제공합니다. HiPPO-LegS는 timescale robustness 시간 스케일 강건성, fast updates 빠른 업데이트, 그리고 bounded gradients 제한된 그라디언트라는 이론적 이점을 누린다.
Memory dynamics 메모리 동역학을 recurrent neural networks 순환 신경망에 통합함으로써, HiPPO RNNs는 복잡한 temporal dependencies 시간적 종속성을 empirically 경험적으로 포착할 수 있다. Permuted MNIST 벤치마트 데이터셋에서, HiPPO-LegS는 98.3%라는 SOTA accuracy 정확도를 기록한다. 마지막으로, out-of-distribution timescales 분포 외 시간 스케일 및 missing data 누락된 데이터에 대한 강건성을 테스트하는 novel trajectory classification 작업에서, HiPPO-LegS는 RNN 및 neural ODE 베이스라인들보다 25-40% 더 높은 정확도로 뛰어난 성능을 보인다.

2. The HiPPO Framework: High-order Polynomial Projection Operators

저자들은 memory representations를 online function approximations with projections의 문제로 접근한다.

2.1. HiPPO Problem Setup

주어진 input function $f(t) \in \mathbb{R}$ on $t \geq 0$에 대해서, 많은 문제들은 모든 시간 $t \geq 0$에 대한 cumulative history 누적된 역사 $f_{\leq t} := f(x) |_{x \leq t} $에 대한 연산을 요구한다. 이는 현재까지 주어진 입력을 이해하고 미래의 예측을 수행하기 위함이다. 함수들의 space는 매우 크기 때문에 역사는 완벽하게 기억될 수 없으며 따라서 compressed 압축 되어야만 한다. 저자들은 이를 위해서 bounded dimension의 subspace로의 projection에 대한 일반적인 접근을 제안한다. 따라서 목표는 역사의 representation을 online으로 유지함이다.

Function Approximation with respect to a Measure

Approximation 근사의 질을 평가하기 위해서는 function space에서의 거리 정의가 필요하다. Any probability measure $\mu$ on [0, $\infty$)는 inner product $<f, f >_{\mu} = \int_0^{\infty} f(x) g(x) d \mu(x) $와 space of square integrable functions를 가진다. 이를 통해 Hibert space structure $\mathcal{H}_{\mu}$와 이에 대응하는 norm인 $ ||f||_{L_{2}(\mu)} = <f, f >_{\mu}^{1/2}$를 유도한다.

여기서 말하는 힐베르트 공간은 수학과스럽게 찾아보면 completeness와 inner product space 등 개념이 나오는데 이를 온전하게 혹은 엄밀하게 (definition, theorem, proof를 거친) 이해하려고 시도 하다 보면 한도 끝도 없으므로 간략하게 설명한다. 우리가 흔히 아는 Euclidean space 유클리드 공간의 일반화된 버젼이 힐베르트 공간이다. 유클리드 공간은 엄밀하지 않지만 쉽게 설명하자면 우리가 흔히 아는 Cartesian coordinate나 Polar Coordinate로 나타내는 유한한 차원을 가진 벡터 공간이다. 구체적인 예를 들면 2차원 평면이나 3차원 공간에서 벡터를 표현하는 방식이다. 힐베르트 공간은 이를 무한 차원으로 확장하고 함수 공간도 다루게 된다.

그래서 결국 하고 싶은게 무엇이냐면, 벡터 끼리 거리를 최소화 하듯이 함수 간의 거리를 최소화 하고 싶기 때문에, 우선 함수 간의 거리를 설정한다는 뜻이다. 기준이 되는 거리가 정의되었으니 이제 이 기준으로 거리를 최소화하는 함수를 찾게 된다.

Polynomial Basis Expansion

Any $N$-dimensional subspace $\mathcal{G}$는 approximation에 적합한 후보다. $N$은 근사의 order인데 이는 곧 압축의 크기다. 해당 논문의 나머지 부분들에서 polynomials를 basis로 삼기 때문에 $\mathcal{G}$은 $N$ 이하의 차수를 갖는 다항식의 집합이다. Polynomial basis는 아주 일반적인데 예를 들어서 unit circle $(e^{(2\pi i x)})^n$에 대한 Fourier basis sin($nx$)와 cos($nx$)는 polynomials로 볼 수 있다.

Online Approximation

Every time $t$에 대해서 $f_{\leq t}$을 근사하므로 measure 측도를 시간에 따라서 달라지도록 설정한다. For every time $t$에 대해서 $\mu^{(t)}$는 supported on ($- \infty, t$]다. 전반적으로 $ || f_{\leq t} - g^{(t)} ||_{L_{2}(\mu)} $ 를 만족하는 $g^{(t)} \in \mathcal{G}$를 찾게 된다. 측도 $\mu$는 input domain의 다양한 부분의 중요성을 제어하고 basis는 허용되는 근사인지를 정의한다. 문제점은 이 최적화 문제를 주어진 $\mu^{(t)}$에 대해서 closed form으로 구할 수 있는지, 그리고 어떻게 coefficients를 $t \rightarrow \infty$일 때 online으로 유지 가능한지의 두 가지다.

2.2. General HiPPO framework

문제 해결에 대한 핵심 아이디어를 간단하게 소개한다. 여러가지의 measure families $\mu(t)$에 대한 간단하고 일반적인 전략을 제시한다. 이는 well-studied orthogonal polynomials와 연관된 transformers을 signal processing 신호처리에 기초한다. Appendix A.1에 자세하게 소개된 기존의 sliding transforms의 몇몇 방법과는 다르다. 예를 들어서, 시간에 따라 변하는 측도라는 개념을 통해 $\mu(t)$를 더 적절하게 선택할 수 있으며, 이는 질적으로 different behavior 다른 동작을 하는 solutions 해들을 도출할 수 있다. Appendix C에는 본 프레임워크의 전체 세부 사항과 formalism (수학에서의 formal systems, 형식체계와 관련된 개념)이 포함되어 있다.

Calculating the projection through continuous dynamics.

앞서 언급했듯이 $N$개의 coefficients를 활용한 basis를 통해서 함수를 근사할 수 있다.

처음 $k$ 스텝 동안은 suitable basis 적합한 기저인 $\mathcal{G}$에 속한 $\{ g_n \}_{n<N}$을 선택한다.

Approximation theory의 고전적 기법을 활용하면, natural basis 자연스러운 기저는 측도 $\mu(t)$에 대한 orthogonal polynomials의 집합이 도니다. 이를 통해서 subspace의 orthogonal basis를 형성한다. 그다음 optimal basis expansion의 coefficients는 $ c_n^{(t)} = < f_{\leq t}, g_n >_{\mu^{(t)}} $가 된다.

두 번째 핵심 아이디어는 시간 $t$에서의 projection의 differentiate 미분이다. Inner product $< f_{\leq t}, g_n >_{\mu^{(t)}}$를 적분하면서 미분을 적용하면 self-similar relation $ \frac{d}{dt} c_n^{(t)}$를 $(c_k(t))_{k \in [N]}$와 $f(t)$의 텀들로 표시할 수 있게 된다. 따라서 coefficients $c(t) \in \mathbb{R}^N$은 ODE로 풀수있게 되며 $f(t)$에 결정되는 dynamics 동역학이 된다.

Orthogonal Polynomials

Orthogonality in functions의 핵심 개념도 선형대수의 벡터의 orthogonality와 동일하다.

Inner product의 값이 0이면 둘은 서로 orthogonal이다.

이제 orthogonal polynomials는 다항식인데 서로 orthogonal인 다항식들임을 알 수있다.

전에 동료들에게 Legendre, Hermite, Laguerre, Chebyshev 이정도 함수들을 들었던거 같다.

기억의 의하면 그중에서 르장드르를 가장 흔하게 사용하는듯했다.

The HiPPO abstraction: online function approximation

Definition 1. 주어진 Time-varying measure family $\mu(t)$가 supported on ($- \infty, t$]일 때,

polynomials의 $N$-dimensional subspace $\mathcal{G}$와 continuous function 연속 함수 $f: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}$, HiPPO는 projection operator $\text{proj}_t$와 coefficient extraction operator $\text{coef}_t$ at every time step $t$를 정의한다. 그리고 아래 properties를 만족한다.

(1) $\text{proj}_t$는 시간 $t$까지 제한된 함수 $f_{\leq t} := f(x) |_{x \leq t}$를 취한다. 그리고 이를 polynomial $g^{(t)} \in \mathcal{G}$로 매핑하는데, approximation error인 $ || f_{\leq t} - g^{(t)} ||_{L_2(\mu^{(t)})} $를 최소화한다.

(2) $\text{coef}_t$: $\mathcal{G} \rightarrow \mathbb{R}^{N}$은 polynomial $g^{(t)}$를 coefficients $ c(t) \in \mathbb{R}^{N} $로 매핑한다. 이 coeffieints는 measure $\mu(t)$와 함께 정의되는 orthogonal polynoimials의 basis의 coefficients다.

위 두 연산의 composition인 coef $\circ$ proj 을 hippo라고 한다.

hippo는 (hippo$(f)$)($t$) = $\text{coef}_t$($\text{proj}_t (f))$다.

이는 곧 hippo가 함수 $f: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R} $를 optimal projection cofficients $ c: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}^{N}$으로 매핑하는 함수라는 뜻이다.

일반적인 $y = f(x) = x + 1$ 같은 함수가 두 실수 집합 사이를 $\mathbb{R} \rightarrow \mathbb{R} $로 매핑하는 것 처럼 함수 공간 끼리 서로 매핑하는 함수가 hippo라고 생각하면 된다.

모든 $t$에 대해서 optimal projection $\text{proj}_t (f)$)은 앞의 innter products에 의해서 잘 정의되어 있지만 계산할 때 추적할 수 없다. Appendix D에 자세히 설명된 저자들의 derivations에 의하면 coefficients function $c(t)$ = $\text{coef}_t$($\text{proj}_t (f))$는 다음의 ODE 형식을 만족한다.

$\frac{d}{dt} c(t) = A(t)c(t) + B(t)f(t) $

이때, $A(t) \in \mathbb{R}^{N \times N}, B(t) \in \mathbb{R}^{N \times 1}$다.

ODE를 풂으로써 $c(t)$를 online으로 추적할 수 있음을 보인다.

$\frac{d}{dt} c(t) = A(t)c(t) + B(t)f(t) $ 이 부분이 HiPPO와 SSM (State-Space Model) 사이를 연결하는 지점이다.

일반적인 SSM이 다음과 같다고 하자.

$x$는 state 상태, $y$는 output 결과, $u$는 input 입력이고 $x' = \frac{d}{dt} x(t)$다.

$x'(t) = A(t)x(t) + B(t)u(t)$

$y(t) = C(t)x(t) + D(t)u(t)$

$c(t)$를 상태로, $f(t)$를 입력으로 보면 $x(t)' = A(t)x(t) + B(t)u(t)$와 동일함을 알 수 있다.

아래 Figure 1은 위에서 설명한 HiPPO의 proejction과 coefficient 과정을 보여준다.

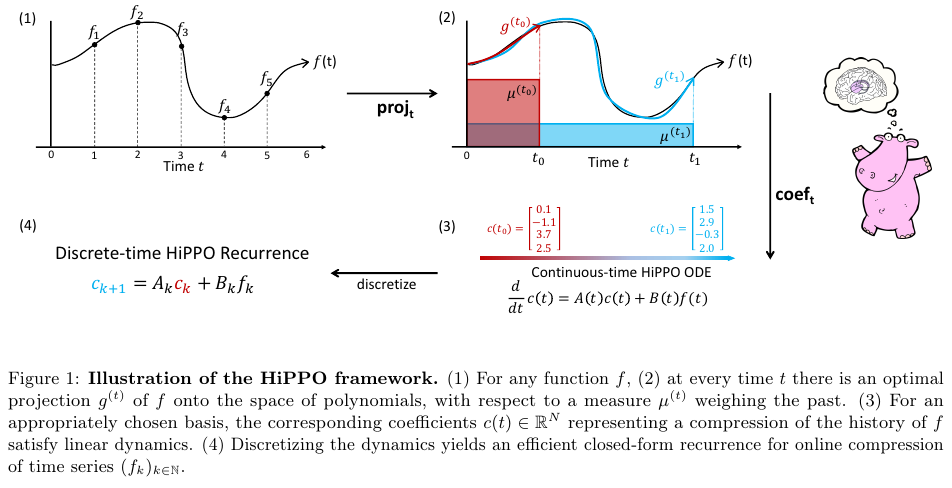
2.3. High Order Proejction: Measure Families and HiPPO ODEs

저자들은 2가지 natural sliding window measures와 corresponding projection operators를 소개한다.

이러한 메모리 메카니즘에 대한 통합된 시각은 Appendieces D.1과 D.2에 제시되었듯이 closed-form의 해를 유도할 수 있다.

첫 번째는 Legendre Memory Unit (LMU)로 HiPPO 프레임워크의 보편성으로 표현할 수 있다.

이에 자세한 내용과 추가적인 Fourier나 Chebyshev에 대한 유도는 Appendix D에 포함되어있다.

Translated Legendre (LegT) measures는 [$t - \theta, t$]의 최근 역사에 대해 uniform weight를 부여한다.

하이퍼파라미터 $\theta$는 sliding window의 길이를 조절하거나 요약된 역사의 길이를 조절한다.

Translated Laguerre (LagT) measures는 [$t - \theta, t$]의 최근 역사에 대해 exponential decay를 부여한다.

이는 최근의 역사에 더 많은 가중치를 부여하게 되는데, 이를 더 중요하게 여긴다는 것과 동일하다.

LegT: $\mu^{(t)}(x) = \frac{1}{\theta} \mathbb{I}_{\left[t - \theta, t\right] (x) } $

LagT: $\mu^{(t)}(x) = exp(-(t - x)) \mathbb{I}_{\left[ - \infty, t\right] (x) } $

$$
=
\begin{cases}
exp(x - t) \,\,\, ,if \,\, x \leq t\\
0 \,\, ,if \,\,\, x \gt t\\
\end{cases}
$$

Theorem 1. For LegT and LagT measures, the hippo operators satisfying Definition 1 are given by linear time-invariant (LTI) ODEs $\frac{d}{dt} c(t) = -Ac(t) + Bf(t)$,
where $A \in \mathbb{R}^{N \times N}, B \in \mathbb{R}^{N \times 1}$.

LegT:
$$
A_{nk} = \frac{1}{\theta}
\begin{cases}
(-1)^{n - k}(2n + 1) \,\,\, ,if \,\, n \geq k\\
2n + 1 \,\, ,if \,\,\, n \lt k\\
\end{cases}
$$

$$ B_{n} = \frac{1}{\theta} (-1)^{n}(2n + 1) $$ ... (1)

LagT:

$$
A_{nk} = \frac{1}{\theta}
\begin{cases}
1 \,\,\, ,if \,\, n \geq k\\
0 \,\, ,if \,\,\, n \lt k\\
\end{cases}
$$

$$ B_{n} = 1 $$ ... (2)

Equation (1)은 the LMU update를 증명한다. 추가적으로 저자들의 유도는 Appendix D.1에 있는데 projections의 바깥의 또 다른 근사의 근원을 보여준다. This sliding window update rule은 $f (t − \theta)$의 접근을 요구하는데 가능하지 않다. 대신 the current coefficients $c(t)$가 $f(x)_{x \leq t}$가 충분히 정확하기 때문에 $f (t − \theta)$를 회복할 수 있다.

2.4. HiPPO recurrences: from Continuous to Discrete Time with ODE Discretization

실제 데이터는 이산형이기 때문에 HiPPO의 프로제젝션 연산을 어떻게 표준적인 기법으로 이산화할 수 있을지 논한다. Continuous-time HiPPO ODEs는 discrete-time linear recurrences로 변한다.

연속형에서 이러한 연산은 input function $f(t)$를 소비하고 output function인 $c(t)$를 생산한다.

Discrete time case에서 (i)은 input sequence $(f_k)_{ k \in N}$, (ii) implicitly 함수 $f(t)$를 정의하는데 이때 $f(k \cdot \Delta t) = f_k$ for some step size $\Delta t$, (iii) 함수 $c(t)$를 생산하는데 이때 ODE dynamics를 거친다. (iv) 다시 discretizes back to an output sequence $c_k := c(k \cdot \Delta t)$

이산화의 기본적 방법은 ODE $\frac{d}{dt}c(t) = u(t, c(t), f(t))$을 이산화하고 스텝 사이즈를 $\Delta t$로 고른다. 이산화된 업데이트는 $c(t + \Delta t) = c(t) + \Delta t \cdot u(t, c(t), f(t))$로 수행한다. 일반적으로 이 과정은 discretization step size 하이퍼파라미터인 $\Delta t$에 sensitive 민감하다.

마지막으로 missing values 결측치 혹은 누락값이 있더라도 타임스탬프가 있는 데이터를 원활히 처리할 수 있는 방법에 유의해야한다. 타임스탬프 간의 차이는 이산화에 사용할 (적응형) $\Delta t$를 나타낸다. Appendix B.3에 이산화에 대한 전체 내용이 자세하게 포함되어 있다.

2.5. Low Order Projection: Memory Mechanisms of Gated RNNs

스페셜 케이스의 하나로 higher order가 아닌 경우에는 어떻게 되는지 확인한다. 구체적으로 N = 1로 설정한다. 그러면 이산화된 버젼의 HiPPO-LagT (2)는 $c(t + \Delta t) = c(t)+ \Delta t ( - Ac(t) + Bf(t)) = (1 - \Delta t) c(t) + \Delta t f(t) $로 변하는데 그 이유는 A = B = 1 이기 때문이다. If the inputs $f(t)$은 hidden state $c(t)$에 의존한다면 the discretization step size $\Delta t$이 input $f(t)$ and $state c(t)$의 함수로서 적응적으로 선택된다. 이는 곧 gated RNN 구조다.예를 들어서 multiple units를 쌓고 특정한 업데이트 함수를 선택함으로써 GRU update cell을 얻을 수 있고 이를 스페셜 케이스 중 하나다. One hidden feature를 사용해서 high order polynomials로 project하는 HiPPO 대신, 여기서는 많은 hidden features를 사용하고 degree 1인 project한다. 이런 관점은 고전적인 기법들이 어떻게 first principles에서 도출될 수 있는지 보여줌으로써 이러한 기법들을 조명한다.

3. HiPPO-LegS: Scaled Measures for Timescale Robustness

Online function approximation과 memory는 서로 밀접하게 연결되어있기에 더 나은 이론적 성질을 지닌 메모리 메커니즘을 생성하기 위해서는, 간단하게 적절한 measure를 선택함으로써 달성할 수 있다. Signal processing에서 sliding windows (Appendix A.1)는 흔한 것으로 메모리를 위한 더 직관적인 접근법은 window를 시간에 따라서 scale하여 forgetting을 피하는 것이다.

저자들의 새로운 방법인 scaled Legendre measure (LegS)는 모든 역사 [$0, t$]: $\mu^{(t)} = \frac{1}{t} \mathbb{I}_{[0, t]}$에 대해서 uniform weight 동일한 가중치를 부여한다. Appendix D와 Figure 5에서 LegS, LegT, LagT를 비교한다.

Theorem 2. The continuous- and discrete- time dynamics for HiPPO-LegS는 다음과 같이 표기할 수 있다.

LagS:

$$ \frac{d}{dt}c(t) = - \frac{1}{t} Ac(t) + \frac{1}{t} Bf(t) ... (3) $$

$$ c_{k + 1} = (1 - \frac{A}{k}) c_k + \frac{1}{k} Bf_k ... (4) $$

$$
A_{nk} =
\begin{cases}
(2n + 1)^{1/2} (2k + 1)^{1/2} \,\,\, ,if \,\, n \gt k\\
n + 1 \,\, ,if \,\,\, n == k, \\
0 \,\, ,if \,\,\, n \lt k\\
\end{cases}
$$

$$ B_{n} = (2n + 1)^{1/2} $$ ... (5)

HiPPO-LegS는 입력 데이터의 timescale에 대해서 invariant하며 빠르게 계산이 가능하며, bounded gradients와 bounded approximation error를 가진다. 모든 증명은 Appendix E에 있다.

Timescale robustness

LegS의 window size는 적응적이므로 이러한 measure에 대한 projection은 직관적으로 timescale에 robust 강건하다. HiPPO-LegS 연산은 timescale-equivariant라고 할 수 있다. 입력 $f$의 확장이 approximation coefficients를 변경하지 않는다.

Proposition 3. For any scalar $\alpha > 0$, if $h(t) = f(\alpha t)$n then hippo$(h)(t)$ = hippo$(f)(\alpha)$

다시 말해서, any dilation function $\gamma : t \rightarrow \alpha t$에 대새 hippo($f \circ \gamma$) = hippo($f) \circ (\gamma$)

이는 HiPPO-LegS가 timescale hyperparameters를 갖지 않음을 반영한다. 반면에 LegT는 window size에 대한 하이퍼파라미터인 $\theta$를 가지며, LegT와 LagT는 step size 하이퍼파라미터인 $\Delta t$를 갖는다.

Comtutationaly efficiency

이산형 HiPPO를 업데이트하기 위해서는 주로 discretized square matrix A의 행렬곱 연산을 수행한다. 일반적으로 임의의 step sizes $\Delta t$에 대해서 $ I + \Delta t \cdot A$와 $ (I - \Delta t \cdot A)^{-1} $ 형태의 곱을 요구한다. 이는 $O(N^2)$의 연산이다. 반면에 LegS는 특별한 구조의 고정된 A 행렬을 가지므로 훨씬 빠르다.

Proposition 4. Under any generalized bilinear transform discretization (cf. Appendix B.3), each step of the HiPPO-LegS recurrence in equation (4) can be computed in $O(N )$ operations

Gradient flow.

RNNs에서의 vanishing gradient을 해결하기 위한 많은 시도들이 있었다. LegS는 메모리에 대해서 설계되었으므로 vanishing gradient문제를 피한다.

Proposition 5. For any times $t_0 < t_1$ , the gradient norm of HiPPO-LegS operator for the output at time $t_1$
with respect to input at time $t_0$ is $|| \frac{\partial_c (t_1)}{\partial_f (t_0)} ||$ = $ \Theta(1 / t_1) $.

Approximation error bounds.

LegS의 error rate of LegS는 the smoothness of the input와 함께 감소한다.

Proposition 6. $f : \mathbb{R_{+}} → \mathbb{R} $인 미분 가능한 함수일 때, $g^{(t)}$는 maximum polynomial degree가 $N - 1$인 HiPPO-LegS에 의한 projection function at time $t$다. 만약 $f$가 $L-Lipschitz$라면 $ || f_{\leq t} - g^{(t)} || = O(tL / \sqrt{N}) $이다. 만약 $f$가 order-k bounded derivatives라면 $ || f_{\leq t} - g^{(t)} || = O(t^{k} N^{-k+1/2}) $가 성립한다.

L-Lipschitz

$f : \mathbb{R}^{n} → \mathbb{R} $가 L-Lipschitz다 라고 하기 위해서는 다음의 조건을 만족해야 한다.

$\forall x, y \in \mathbb{R}^{n} $에 대해서 $ || f(x) - f(y)|| \leq L \cdot || x - y || $

이때 $|| \cdot ||$은 보통 Euclidean norm을 사용하며, $L \geq 0$인 $L$을 Lipschitz constant라고 한다.

함수의 변화율이 너무 급격하지 않도록 제한하는 조건이다.

4. Empirical Validation

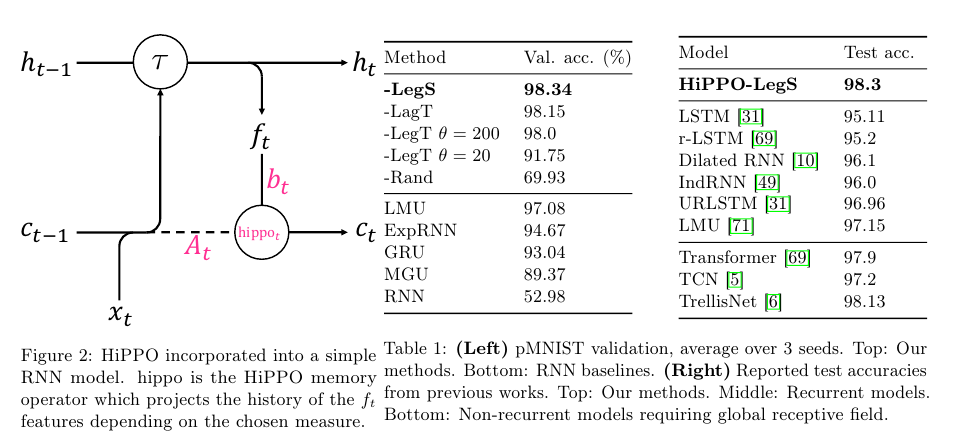
Figure 2에서는 RNN과 HiPPO을 결합한 모습을 보여준다.

Table 1에서는 pMNIST 데이터에 대한 validation accuracy와 test accuracy를 보여준다.

LegS가 가장 좋은 성능을 달성함을 확인할 수 있다.

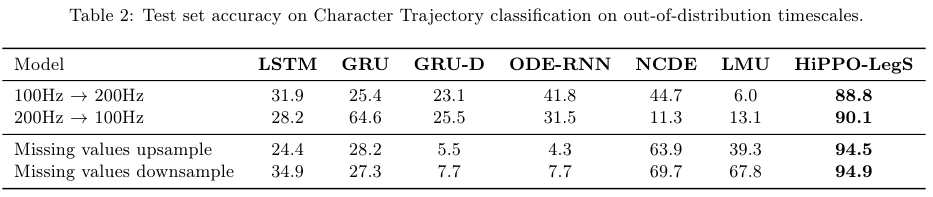
Table 2에서는 out-of-distribution timescales에 대한 Character Trajectory classification의 결과를 보여준다.

HiPPO-LegS가 가장 강건함을 알 수 있다.

Table 3에서는 hidden units가 256일 때 1백만의 time steps가 지난 다음 함수의 approximation error (MSE로 측정된)를 보여준다. Speed 항목을 보면 HiPPO-LegS가 LSTM이나 LMU보다 훨씬 빠른 속도를 지녔으면서도 MSE가 작음을 알 수 있다.

References:

https://velog.io/@jpseo99/HiPPO-Recurrent-Memory-with-Optimal-Polynomial-Projections

https://haawron.tistory.com/50

https://en.wikipedia.org/wiki/Hilbert_space

Mathematics for Physicists: Introductory Concepts and Methods, Alexander Atland

https://en.wikipedia.org/wiki/Orthogonal_polynomials

https://huggingface.co/blog/lbourdois/get-on-the-ssm-train

https://en.wikipedia.org/wiki/State-space_representation

https://en.wikipedia.org/wiki/Lipschitz_continuity