https://arsetstudium.tistory.com/46 에서 설명했던 User-based Collaborativg Filtering과 Item-based Collaborativg Filtering을 파이썬으로 구현한다.
학습데이터로는 MovieLens 1M 데이터를 사용한다.
https://grouplens.org/datasets/movielens/1m/
원본 데이터는 아마 .dat 형태라서 파이썬의 open 함수로 열어서 csv로 변형했던걸로 기억한다.
open과 split 등으로 잘 변환해서 pandas의 dataframe 형태로 만들고 저장하면 된다.
Load Data
import os
import numpy as np
import pandas as pd
import sklearn
ratings = pd.read_csv(os.path.join(data_path, 'ratings.csv'), index_col=0)
ratings
>>
userId movieId rating timestamp
0 1 1193 5.0 978300760
1 1 661 3.0 978302109
2 1 914 3.0 978301968
3 1 3408 4.0 978300275
4 1 2355 5.0 978824291
... ... ... ... ...
1000204 6040 1091 1.0 956716541
1000205 6040 1094 5.0 956704887
1000206 6040 562 5.0 956704746
1000207 6040 1096 4.0 956715648
1000208 6040 1097 4.0 956715569
ratings.csv는 userId, movieId, rating, timestamp의 네 가지 컬럼으로 구성된 데이터임을 알 수 있다.
User-Item interaction의 숫자는 1,000,208개임을 알 수 있다.
왜 1M이란 이름이 붙었는지 알 수 있는 대목이다.
ratings['userId'].max()
>>
6040
ratings['movieId'].max()
>>
3952
userId와 movieId의 max 값을 출력해봤는데 각각 6040과 3952다.
각각의 시작 값이 1이라고 하면 userId와 movieId (itemId)의 가능한 모든 조합의 수는 6040 x 3952다.
(가능한 모든 조합의 수는 Two disjoint sets의 Bipartite graph로 표현할 수 있고 cartesian product라고도 한다.)
계산하면 23,870,080으로 약 2천 387만이다. 전체 2,387만 cells 중에서 1만개만이 값 (점수)가 있고 나머지는 모두 0이란 소리다.
이런 추천 시스템의 특성을 sparsity라고도 한다.
가능한 가지 수에 비해서 데이터가 너무나 부족하단 뜻이다.
# info 함수로 column별 데이터 타입 그리고 메모리량을 알 수 있다.
ratings.info()
>>
<class 'pandas.core.frame.DataFrame'>
Index: 1000209 entries, 0 to 1000208
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 userId 1000209 non-null int64
1 movieId 1000209 non-null int64
2 rating 1000209 non-null float64
3 timestamp 1000209 non-null int64
dtypes: float64(1), int64(3)
memory usage: 38.2 MB
# rating이 몇점 단위인지 확인한다.
# 별점 반개, 0.5점이 없는 5점 척도다.
ratings['rating'].unique()
>> array([5., 3., 4., 2., 1.])
이번에는 영화 자체에 대한 데이터가 담긴 movies를 불러오고 살펴본다.
movies = pd.read_csv(os.path.join(data_path, 'movies.csv'), index_col=0)
movies
>>
movieId title genre
0 1 Toy Story (1995) Animation|Children's|Comedy
1 2 Jumanji (1995) Adventure|Children's|Fantasy
2 3 Grumpier Old Men (1995) Comedy|Romance
3 4 Waiting to Exhale (1995) Comedy|Drama
4 5 Father of the Bride Part II (1995) Comedy
... ... ... ...
3878 3948 Meet the Parents (2000) Comedy
3879 3949 Requiem for a Dream (2000) Drama
3880 3950 Tigerland (2000) Drama
3881 3951 Two Family House (2000) Drama
3882 3952 Contender, The (2000) Drama|Thriller
3883 rows × 3 columns
정수 형태의 movieId, 영화의 제목 (상영연도), 장르의 세 가지 컬럼으로 이루어져있음을 알 수 있다.
Pre-process the Data
users_uniq = ratings['userId'].unique()
items_uniq = ratings['movieId'].unique()
"""
0번째 user가 만약 id가 1193이라면 0으로 매핑한다.
0번째 item이 만약 id가 11593이라면 0으로 매핑한다.
원래 user id와 바뀐 user id,
그리고 원래의 item(movie) id와 바뀐 item id가 모두 필요한데
이는 추천 이후 다시 원래의 user와 id로 변경하여 주어야 하기 때문이다.
"""
def remap(uniq_values):
v2idx = {}
idx2v = {}
for idx, v in enumerate(uniq_values):
v2idx[v] = idx # v 값을 주면 새로운 id인 idx 리턴
idx2v[idx] = v # 바뀐 값인, idx 값을 주면 원래 v를 리턴
return v2idx, idx2v
user_orig2new, user_new2orig = remap(users_uniq)
item_orig2new, item_new2orig = remap(items_uniq)
그 다음 원래의 rating을 새로운 idx들로 바꾼 df로 변환해야 한다.
def make_new_id(name, name_dict):
return name_dict[name]
ratings['user'] = ratings.apply(lambda x: make_new_id(x['userId'], user_orig2new),
axis=1)
ratings['item'] = ratings.apply(lambda x: make_new_id(x['movieId'], item_orig2new),
axis=1)
ratings
>>
userId movieId rating timestamp user item
0 1 1193 5.0 978300760 0 0
1 1 661 3.0 978302109 0 1
2 1 914 3.0 978301968 0 2
3 1 3408 4.0 978300275 0 3
4 1 2355 5.0 978824291 0 4
... ... ... ... ... ... ...
1000204 6040 1091 1.0 956716541 6039 772
1000205 6040 1094 5.0 956704887 6039 1106
1000206 6040 562 5.0 956704746 6039 365
1000207 6040 1096 4.0 956715648 6039 152
1000208 6040 1097 4.0 956715569 6039 26
1000209 rows × 6 columns
0부터 시작하고, 사이사이에 빈값이 없도록 바꾼 userId와 movieId를 각각 user와 item으로 새로 할당하고 df에 컬럼으로 넣어준다.
User-based Collaborativg Filtering
Cosine similarity와 Pearson Correlation, 그리고 Jaccard Index로 추천을 해보려고 한다.
우선 user-item interaction matrix는 중간에 빈 공간, 즉 0이 많은 행렬이다.
현재 (user, item, rating)으로 되어있는 db의 table 형식 (여기서는 DataFrame)을
matrix 형태로 변경하여 살펴본다.
matrix = ratings.pivot(index='user', columns='item', values='rating')
matrix
>>
item 0 1 2 3 4 5 6 7 8 9 ... 3696 3697 3698 3699 3700 3701 3702 3703 3704 3705
user
0 5.0 3.0 3.0 4.0 5.0 3.0 5.0 5.0 4.0 4.0 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 5.0 NaN NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 NaN NaN NaN NaN 5.0 5.0 NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 NaN NaN NaN 3.0 5.0 NaN NaN NaN NaN 4.0 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
6035 5.0 NaN 3.0 4.0 4.0 5.0 NaN NaN 5.0 NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6036 4.0 NaN NaN NaN NaN NaN NaN 4.0 NaN 4.0 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6037 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6038 NaN 3.0 4.0 NaN NaN 4.0 NaN 4.0 NaN 4.0 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6039 4.0 NaN NaN NaN NaN NaN NaN NaN NaN 5.0 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6040 rows × 3706 columns
Row에 user, Column에 item이 할당된 형태임을 알 수 있다.
User가 사용하지 않은 item에 대해선 값이 없으므로 NaN이 할당되는데, 이를 모두 0으로 변경하여 다시 살펴본다.
matrix = matrix.fillna(0)
matrix
>>
item 0 1 2 3 4 5 6 7 8 9 ... 3696 3697 3698 3699 3700 3701 3702 3703 3704 3705
user
0 5.0 3.0 3.0 4.0 5.0 3.0 5.0 5.0 4.0 4.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 5.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 0.0 0.0 0.0 0.0 5.0 5.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
4 0.0 0.0 0.0 3.0 5.0 0.0 0.0 0.0 0.0 4.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
6035 5.0 0.0 3.0 4.0 4.0 5.0 0.0 0.0 5.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
6036 4.0 0.0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 4.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
6037 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
6038 0.0 3.0 4.0 0.0 0.0 4.0 0.0 4.0 0.0 4.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
6039 4.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 5.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
6040 rows × 3706 columns
6040 x 3706 matrix가 만들어졌으며 굉장히 많은 값들이 0임을 알 수 있다.
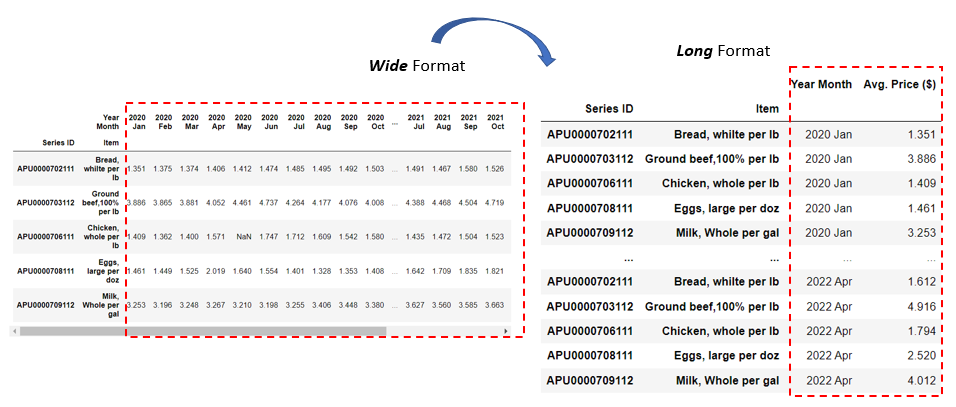
Pandas에서는 pivot table 형태를 Wide Format이라고 한다.
우리가 아는 RDB 형식의 table은 Long Format이라고 한다.
wide to long과 long to wide를 쓸 일이 있을테니 알아두면 좋다.
wide_to_long, unstakc, melt, pivot 등의 명령어를 쓰면 된다.
레퍼런스에 관련된 Towards Data Science와 블로그 링크를 걸어두었다.
이제 다시 matrix 내용으로 돌아와서, 추천과 같은 경우 0들끼리 곱해도 값에 변화가 없기도 하고
정보값이 없는 0들이 굉장히 많은 자리를 차지하고 있기 때문에 메모리의 낭비이다.
보다 효율적인 표현을 위해서 scipy에서 제공하는 sparse matrix로 데이터를 표현할 수 있다.
pandas의 dataframe와 numpy array 모두를 input으로 넣어서 sparse matrix를 만들 수 있다.
from scipy.sparse import csr_matrix
# Pandas Pivot Table에서 csr matrix 생성
csr_matrix(matrix)
>>
<6040x3706 sparse matrix of type '<class 'numpy.float64'>'
with 1000209 stored elements in Compressed Sparse Row format>
# Numpy Array = Pandas Pivot Table의 values에서 csr matrix 생성
csr_matrix(matrix.values)
<6040x3706 sparse matrix of type '<class 'numpy.float64'>'
with 1000209 stored elements in Compressed Sparse Row format>
이번에는 원본 테이블(데이터프레임)에서 만들어본다.
csr_matrix((ratings['rating'].values,
(ratings['user'].values, ratings['item'].values)),
shape=(ratings['user'].nunique(), ratings['item'].nunique()))
>>
<6040x3706 sparse matrix of type '<class 'numpy.float64'>'
with 1000209 stored elements in Compressed Sparse Row format>
# Numpy Array로 만들기
csr_matrix((ratings['rating'].values,
(ratings['user'].values, ratings['item'].values)),
shape=(ratings['user'].nunique(), ratings['item'].nunique())).toarray()
>>
array([[5., 3., 3., ..., 0., 0., 0.],
[5., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 3., 4., ..., 0., 0., 0.],
[4., 0., 0., ..., 0., 0., 0.]])
scipy의 csr_matrix((data, (row_ind, col_ind)), [shape=(M, N)]) arguments를 보면,
data에 value, row_ind에 row, col_ind에 column을 넣으면 된다.
ratings['rating'].values류의 명령어를 이용해서 data를, row에 user를, column에 item을 설정함을 알 수 있다.
toarray() 메소드를 이용해서 원본 matrix와 비교하면 정상적으로 csr_matrix로 전환되고 이를 다시 array로 전환됨을 알 수 있다.
1. Cosine Similarity
우선 scikit-learn의 cosine_similarity를 통해서 user-user similarity matrix를 만들어 본다.
from sklearn.metrics.pairwise import cosine_similarity
cos_sim = cosine_similarity(csr_mat)
cos_sim, cos_sim.shape
>>
(array([[1. , 0.09638153, 0.12060981, ..., 0. , 0.17460369,
0.13359025],
[0.09638153, 1. , 0.1514786 , ..., 0.06611767, 0.0664575 ,
0.21827563],
[0.12060981, 0.1514786 , 1. , ..., 0.12023352, 0.09467506,
0.13314404],
...,
[0. , 0.06611767, 0.12023352, ..., 1. , 0.16171426,
0.09930008],
[0.17460369, 0.0664575 , 0.09467506, ..., 0.16171426, 1. ,
0.22833237],
[0.13359025, 0.21827563, 0.13314404, ..., 0.09930008, 0.22833237,
1. ]]),
(6040, 6040))
https://arsetstudium.tistory.com/46에서 학습한 내용의 경우 users $u$와 $v$가 공통으로 사용한 items의 점수만 사용해서 유사도를 구한다.
하지만 이 경우 0으로 표기된 모든 아이템이나 user $u$만 사용한 아이템이나 user $v$만 사용한 아이템도 모두 사용한다.
코사인 유사도의 분자 부분의 경우 user $u$나 $v$만 사용한 아이템은 element-wise로 곱하면서 0이 되어 사라지지만,
분모의 경우 각자만 사용한 아이템도 모두 사용되어 norm이 계산되기 때문에 공통으로 사용한 items의 점수만 사용한 코사인 유사도 값과 달라지게 된다.
이를 해결하기 위해서 두 유저의 공통된 아이템만을 사용해서 계산하는 함수를 만들어서 다시 계산해보고자 한다.
# user가 사용한 items의 모음을 dictionary 형태로 만든다
user_item_dict = {}
users_uniq = ratings['user'].unique()
# items_uniq = ratings['movieId'].unique()
for user in users_uniq:
user_df = ratings[ratings['user']==user]
# 현재 user가 사용한 아이템들을 뽑아서 딕셔너리에 넣는다.
# 파이썬 set 형태로 넣는다.
user_item_dict[user] = set(user_df['item'].unique())
# user u와 v의 공통된 아이템들을 만들어서
# 코사인 유사도의 denominator를 리턴한다.
def common_norm(matrix, u, v, common_items):
# user 0과 user 1의 공통된 아이템으로 norm을 계산해서 denominator 구하기
norm_u = matrix[u][list(common_items)]
# vector norm aka L2 norm
norm_u = np.linalg.norm(norm_u, 2)
#print("norm_u:",norm_u)
norm_v = matrix[v][list(common_items)]
norm_v = np.linalg.norm(norm_v, 2)
#print("norm_v:",norm_v)
#print("denominator:",norm_u*norm_v)
return norm_u*norm_v
# Denominator array를 리턴한다.
def non_zero_denominator(matrix, users, user_item_dict):
users = list(users)
n_users = len(users)
# 1으로 initialize. diagonal term은 자기자신이라서 모두 1이다.
denom_arr = np.ones((n_users, n_users))
while(users):
u = users.pop(0)
for v in users:
common_items = user_item_dict[u] & user_item_dict[v]
denom = common_norm(matrix, u, v, common_items)
denom_arr[u][v] = denom
denom_arr[v][u] = denom
return denom_arr
# 공통 아이템만을 사용한 코사인 유사도를 구한다.
def nonzero_cosine_similarity(ui_matrix):
# cos sim의 분자 부분
numerator = np.matmul(ui_matrix, ui_matrix.T)
# user들 간의 공통된 아이템으로 norm을 계산해서 denominator 구하기
denominator = non_zero_denominator(ui_matrix, users_uniq, user_item_dict)
sim = numerator / denominator
return sim
cos_sim_common = nonzero_cosine_similarity(matrix.values)
cos_sim_common
>>
array([[9.54000000e+02, 9.84848485e-01, 9.51571736e-01, ...,
nan, 9.72652277e-01, 9.75310751e-01],
[9.84848485e-01, 1.90700000e+03, 9.64280672e-01, ...,
9.80406721e-01, 9.80877776e-01, 9.45492580e-01],
[9.51571736e-01, 9.64280672e-01, 8.25000000e+02, ...,
9.94535842e-01, 9.48274907e-01, 9.26250325e-01],
...,
[ nan, 9.80406721e-01, 9.94535842e-01, ...,
3.12000000e+02, 9.80580676e-01, 8.75412726e-01],
[9.72652277e-01, 9.80877776e-01, 9.48274907e-01, ...,
9.80580676e-01, 1.91500000e+03, 9.70056561e-01],
[9.75310751e-01, 9.45492580e-01, 9.26250325e-01, ...,
8.75412726e-01, 9.70056561e-01, 4.83800000e+03]])
유사도 행렬에 nan의 값이 나오는 경우는 대개 분모가 0인 경우다.
cos_sim_common = np.nan_to_num(cos_sim_common)의 명령어를 수행하면,
nan, inf, -inf 등의 값을 모두 0으로 변환한다.
위의 변환을 수행한 다음 user 0에 대해서 코사인 유사도를 활용하여 추천을 수행한다.
# fillna as -1 whose denominator 0 or user him/herself
sim0 = np.nan_to_num(cos_sim_common[0],-1)
# 자기자신은 -1의 값을 줘서 정렬시에 제외한다.
sim0[0] = -1
sim0
>>array([-1. , 0.98484848, 0.95157174, ..., 0. ,
0.97265228, 0.97531075])
우선 user 0의 user similarity vector를 가져온 다음 자기 자신에 대해서는 -1의 값을 주어 스스로가 추천되는 경우를 방지한다.
# 오름차순이다.
sorted_indices = np.argsort(sim0)
sorted_indices[0:10], sim0[sorted_indices[0:10]]
>> (array([ 0, 940, 5011, 4973, 1059, 4850, 4803, 1122, 4750, 1153],
dtype=int64),
array([-1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))
np.argsort로 정렬된 users similarity score의 index, 즉 유저들을 가져온다.
이때 argosrt의 기본값은 오름차순이므로 유사도가 낮은 순서부터 나열된다.
뒤에 [::-1]을 붙여서 내림차순으로 가져온다.
# np.argsort는 오름차순이므로 [::-1]를 써서 내림차순으로 정렬
sorted_indices = np.argsort(sim0)[::-1]
# 유사도 상위 10명의 사람을 리턴한다.
sorted_indices[0:10], sim0[sorted_indices[0:10]]
>>
(array([3324, 4158, 3618, 1023, 4348, 2557, 1454, 3656, 314, 3615],
dtype=int64),
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]))
상위 10명의 비슷한 users를 가져오고 user-user 코사인 유사도도 출력해서 확인한다.
User 0은 user 3324, 4158, 3618, 1023, 4348, 2557, 1454, 3656, 314, 3615와 유사하며 코사인 유사도는 모두 1이다.
추천 방법1:
가장 높은 유사도 유저의 모든 아이템을 추천
used_items = user_item_dict[0]
most_sim_user = sorted_indices[0]
recommend = user_item_dict[most_sim_user]
print(recommend)
>>
{128, 898, 3, 1157, 1927, 2057, 38, 425, 43, 1708, 178, 445, 317, 454, 1613, 334, 2134, 345, 731, 732, 477, 872, 876, 877, 2158, 372}
가장 높은 유사도를 가진 유저를 가져와서 해당 유저가 사용한 아이템을 모두 추천한다.
# 추천된 아이템의 이름을 출력하는 함수
def print_recommends(recommendations):
print("Recommendations",'='*30)
for idx, rec in enumerate(recommendations):
item_orig = item_new2orig[rec]
item_name = movies[movies['movieId']==item_orig]['title'].item()
print(f"Item {idx+1}: {item_name}")
print_recommends(recommend)
>>
Recommendations ==============================
Item 1: Silence of the Lambs, The (1991)
Item 2: Stir of Echoes (1999)
Item 3: Erin Brockovich (2000)
Item 4: Me, Myself and Irene (2000)
Item 5: Angela's Ashes (1999)
Item 6: Eye of the Beholder (1999)
Item 7: Sixth Sense, The (1999)
Item 8: Out of Africa (1985)
Item 9: Run Lola Run (Lola rennt) (1998)
Item 10: Deep End of the Ocean, The (1999)
Item 11: 28 Days (2000)
Item 12: Summer of Sam (1999)
Item 13: Fight Club (1999)
Item 14: Eyes Wide Shut (1999)
Item 15: Return to Me (2000)
Item 16: Happiness (1998)
Item 17: Flawless (1999)
Item 18: Little Voice (1998)
Item 19: Sister Act (1992)
Item 20: Man on the Moon (1999)
Item 21: Hilary and Jackie (1998)
Item 22: What Lies Beneath (2000)
Item 23: Bone Collector, The (1999)
Item 24: Haunting, The (1999)
Item 25: House on Haunted Hill, The (1999)
Item 26: Boys Don't Cry (1999)
추천 방법2:
가장 높은 유사도 높은 $L$명의 유저들 ($L$ neighbors)의 별점들을 활용하여 아이템의 별점을 예측한다.
그 다음 예측된 별점이 높은 $K$개의 아이템을 추천한다. $\hat{{r}_{ui}}$를 예측하는 방법이다.
L = 5
# np.argsort는 오름차순이므로 [::-1]를 써서 내림차순으로 정렬
sorted_indices = np.argsort(sim0)[::-1]
# 유사도 상위 10명의 사람을 리턴한다.
neighbors = sorted_indices[0:L]
neighbors
>>
array([3324, 4158, 3618, 1023, 4348], dtype=int64)
def predict_rating_sim(sim_mat, ui_matrix, top_neighbors, user):
items_pool = 0
sim_mat = sim_mat[top_neighbors][:,user]
sim_mat = sim_mat.reshape(sim_mat.shape[0], -1)
ui_matrix = ui_matrix[top_neighbors]
pred = sim_mat*ui_matrix
pred = np.nan_to_num(pred)
numerator = pred.sum(axis=0)
denominator = np.abs(sim_mat).sum()
pred = numerator / denominator
pred_items = np.argsort(pred)[::-1]
pred_scores = pred[pred_items]
return pred_items, pred_scores
pred_items, pred_ratings = predict_rating_sim(cos_sim_common, matrix.values, neighbors, 0)
pred_items, pred_ratings
>>
(array([ 128, 425, 3, ..., 2464, 2463, 1852], dtype=int64),
array([2.6, 1.6, 1.6, ..., 0. , 0. , 0. ]))
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Silence of the Lambs, The (1991)
Item 2: Out of Africa (1985)
Item 3: Erin Brockovich (2000)
Item 4: Bone Collector, The (1999)
Item 5: Sixth Sense, The (1999)
Item 6: Groundhog Day (1993)
Item 7: Shakespeare in Love (1998)
Item 8: Leaving Las Vegas (1995)
Item 9: House Party (1990)
Item 10: Stir of Echoes (1999)
2. Pearson Corrleation Coefficient
이번에는 non-zero Pearson Corrleation Coefficient를 활용하여 추천을 수행한다.
scipy의 scipy.stats.pearsonr을 활용하면 Pearson Corrleation의 값 (statistic)을 구할 수 있다.
더불어서 null hypothesis that the distributions underlying the samples are uncorrelated and normally distributed의
검정 역시 수행하며 그와 관련된 p-value로 함께 반환한다.
전통적인 통계학적 방법의 데이터의 분포에 대한 검정이라 ML이나 DL에서는 그리 쓸 일이 없을만한 내용이다.
def non_zero_pearson_values(u, v, ui_matrix, common_items):
numerator_u = ui_matrix[u][list(common_items)]
numerator_u = numerator_u - numerator_u.mean()
numerator_v = ui_matrix[v][list(common_items)]
numerator_v = numerator_v - numerator_v.mean()
numerator = (numerator_u*numerator_v).sum()
denominator = np.linalg.norm(numerator_u,2) * np.linalg.norm(numerator_v,2)
return numerator, denominator
def non_zero_pearson(matrix, users, user_item_dict):
users = list(users)
n_users = len(users)
# 1으로 initialize. diagonal term은 자기자신이라서 모두 1이다.
pearon_arr = np.ones((n_users, n_users))
while(users):
u = users.pop(0)
for v in users:
common_items = user_item_dict[u] & user_item_dict[v]
numer, denom = non_zero_pearson_values(u, v, matrix, common_items)
#print("분자",numer)
#print("분모",denom)
pearon_arr[u][v] = numer/denom
pearon_arr[v][u] = numer/denom
return pearon_arr
>>
array([[ 1. , 0.41666667, -0.33218192, ..., nan,
0.05685735, -0.04351941],
[ 0.41666667, 1. , 0.23683386, ..., -0.5 ,
0.57207755, -0.0271435 ],
[-0.33218192, 0.23683386, 1. , ..., 0.5 ,
0.30927686, -0.39528471],
...,
[ nan, -0.5 , 0.5 , ..., 1. ,
0.27116307, -0.39712226],
[ 0.05685735, 0.57207755, 0.30927686, ..., 0.27116307,
1. , 0.24230884],
[-0.04351941, -0.0271435 , -0.39528471, ..., -0.39712226,
0.24230884, 1. ]])
Cosine similarity처럼 공통된 아이템에 대해서 Pearson correlation을 구한다.
# fillna as -1 whose denominator 0 or user him/herself
sim0 = np.nan_to_num(pearson_corr[0],-1)
# 자기자신은 -1의 값을 줘서 정렬시에 제외한다.
sim0[0] = -1
L = 5
# np.argsort는 오름차순이므로 [::-1]를 써서 내림차순으로 정렬
sorted_indices = np.argsort(sim0)[::-1]
# 유사도 상위 10명의 사람을 리턴한다.
neighbors = sorted_indices[0:L]
pred_items, pred_ratings = predict_rating_sim(pearson_corr, matrix.values, neighbors, 0)
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Star Wars: Episode V - The Empire Strikes Back (1980)
Item 2: Saving Private Ryan (1998)
Item 3: Back to the Future (1985)
Item 4: American Beauty (1999)
Item 5: Four Weddings and a Funeral (1994)
Item 6: Groundhog Day (1993)
Item 7: African Queen, The (1951)
Item 8: Air Force One (1997)
Item 9: Searchers, The (1956)
Item 10: Clueless (1995)
위에서 구한 피어슨 상관관계를 활용하여 user 0에 대해서 추천을 수행한다.
# user 1에 대해서, 30 neighbors, 15 items 추천
user = 1
L = 30
neighbors = get_similar_users(pearson_corr, user, L)
pred_items, pred_ratings = predict_rating_sim(pearson_corr, matrix.values, neighbors, 0)
K = 15
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Five Wives, Three Secretaries and Me (1998)
Item 2: Contender, The (2000)
Item 3: Superman III (1983)
Item 4: Brazil (1985)
Item 5: Manchurian Candidate, The (1962)
Item 6: Lifeboat (1944)
Item 7: Purple Noon (1960)
Item 8: Double Indemnity (1944)
Item 9: Odd Couple, The (1968)
Item 10: Thin Blue Line, The (1988)
Item 11: No Way Out (1987)
Item 12: ...And Justice for All (1979)
Item 13: Nikita (La Femme Nikita) (1990)
Item 14: Touch of Evil (1958)
Item 15: Three Amigos! (1986)
이번에는 user 1에 대해서 30명의 neighbors를 구한 다음,
아이템의 별점을 예측해서 상위 15개의 아이템을 추천하는 코드와 그 결과다.
3. Jaccard Index = Jaccard Similarity
이번에는 Jaccard Index를 활용하여 추천을 수행한다.
def jaccard_similarity(u, v, interaction_dict):
numerator = interaction_dict[u].intersection(interaction_dict[v])
denominator = interaction_dict[u].union(interaction_dict[v])
return len(numerator)/len(denominator)
def make_jaccard_matrix(users, interaction_dict):
users = list(users)
n_users = len(users)
# 1으로 initialize. diagonal term은 자기자신이라서 모두 1이다.
jaccard_matrix = np.ones((n_users, n_users))
while(users):
u = users.pop(0)
for v in users:
jaccard_value = jaccard_similarity(u, v, interaction_dict)
jaccard_matrix[u][v] = jaccard_value
jaccard_matrix[v][u] = jaccard_value
return jaccard_matrix
jaccard_mat = make_jaccard_matrix(users_uniq, user_item_dict)
jaccard_mat
>>
array([[1. , 0.04 , 0.06122449, ..., 0. , 0.0931677 ,
0.04509284],
[0.04 , 1. , 0.07142857, ..., 0.02054795, 0.03278689,
0.11111111],
[0.06122449, 0.07142857, 1. , ..., 0.04411765, 0.04819277,
0.05376344],
...,
[0. , 0.02054795, 0.04411765, ..., 1. , 0.05147059,
0.03142857],
[0.0931677 , 0.03278689, 0.04819277, ..., 0.05147059, 1. ,
0.09692671],
[0.04509284, 0.11111111, 0.05376344, ..., 0.03142857, 0.09692671,
1. ]])
user = 1
L = 5
neighbors = get_similar_users(jaccard_mat, user, L)
pred_items, pred_ratings = predict_rating_sim(jaccard_mat, matrix.values, neighbors, 0)
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Hunt for Red October, The (1990)
Item 2: Braveheart (1995)
Item 3: True Lies (1994)
Item 4: Matrix, The (1999)
Item 5: Saving Private Ryan (1998)
Item 6: Shawshank Redemption, The (1994)
Item 7: Air Force One (1997)
Item 8: Backdraft (1991)
Item 9: Terminator 2: Judgment Day (1991)
Item 10: Men in Black (1997)
자카드 인덱스 방법은 모든 아이템의 rating을 동등하게 카운트한다고도 볼 수 있다.
별점을 1점을 매겨도 5점을 매겨도 모두 사용했다는 점에만 집중하기 때문이다.
별점이 낮은 아이템이 과대대표된다고 느껴질 경우,
유저가 별점을 매긴 아이템들 중에서 3점 이상을 준 아이템만 남기는식으로 필터링을 해서
확실하게 positive feedback을 준, 한 마디로 좋아하거나 선호한다고 생각할 수 있는 아이템만을 이용해서 추천을 수행할 수도 있다.
Item-based Collaborativg Filtering
이번에는 Item-based CF로, user-baed와 마찬가지로 세 가지의 유사도;
Cosine similarity와 Pearson Correlation, 그리고 Jaccard Index를 통해 추천을 해보려고 한다.
item_user_dict = {}
items_uniq = ratings['item'].unique()
# items_uniq = ratings['movieId'].unique()
for item in items_uniq:
item_df = ratings[ratings['item']==item]
# 현재 user가 사용한 아이템들을 뽑아서 딕셔너리에 넣는다.
# 파이썬 set 형태로 넣는다.
item_user_dict[item] = set(item_df['user'].unique())
def item_nonzero_cosine_similarity(ui_matrix):
# cos sim의 분자 부분
# ui_matrix.T = iu_matrix
iu_matrix = ui_matrix.T
numerator = np.matmul(iu_matrix, iu_matrix.T)
# user들 간의 공통된 아이템으로 norm을 계산해서 denominator 구하기
denominator = non_zero_denominator(iu_matrix, items_uniq, item_user_dict)
sim = numerator / denominator
return sim
1. Cosine Similarity
cos_sim_item = item_nonzero_cosine_similarity(matrix.values)
cos_sim_item
>>
array([[3.43300000e+04, 9.55560111e-01, 9.66391644e-01, ...,
nan, 1.00000000e+00, nan],
[9.55560111e-01, 6.85100000e+03, 9.38279980e-01, ...,
nan, nan, nan],
[9.66391644e-01, 9.38279980e-01, 1.14600000e+04, ...,
nan, nan, nan],
...,
[ nan, nan, nan, ...,
1.00000000e+00, nan, nan],
[1.00000000e+00, nan, nan, ...,
nan, 2.50000000e+01, nan],
[ nan, nan, nan, ...,
nan, nan, 1.60000000e+01]])
Cosine similarity matrix의 diagonal term이 1이 아닌데, 이는 어차피 쓸 항목이 아니라서 값을 업데이트 하지 않았기 때문이다. 어차피 get_similar_items에서 자기 자신의 순서에는 -1의 값을 대입해서 제외한다.
def get_similar_items(sim_mat, item, L):
# fillna as -1 whose denominator 0 or user him/herself
sims = np.nan_to_num(sim_mat[item], -1)
# 자기자신은 -1의 값을 줘서 정렬시에 제외한다.
sims[item] = -1
# np.argsort는 오름차순이므로 [::-1]를 써서 내림차순으로 정렬
sorted_indices = np.argsort(sims)[::-1]
# 유사도 상위 10명의 사람을 리턴한다.
neighbors = sorted_indices[0:L]
return neighbors
item = 0
L = 20
# 유사도가 높은 상위 5개의 items
neighbors = get_similar_items(cos_sim_item, item, L)
pred_items, pred_ratings = predict_rating_sim_item(cos_sim_item, matrix.values.T, neighbors, 0)
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Airplane! (1980)
Item 2: My Fair Lady (1964)
Item 3: Princess Bride, The (1987)
Item 4: Erin Brockovich (2000)
Item 5: Beauty and the Beast (1991)
Item 6: Ben-Hur (1959)
Item 7: James and the Giant Peach (1996)
Item 8: Ferris Bueller's Day Off (1986)
Item 9: Gigi (1958)
Item 10: One Flew Over the Cuckoo's Nest (1975)
Users와 ui_matrix를 기준으로 작성한 함수기 때문에, users를 items로 바꾸고 ui_matrix를 iu_matrix로,
user_item_dict을 item_user_dict으로 바꿔서 넣으면 원하는 값을 얻을 수 있다.
행렬의 transpose는 간단하게 .T로 구할 수 있다. iu_matrix = ui_matrx.T다.
2. Pearson Corrleation Coefficient
pearson_corr_item = non_zero_pearson(matrix.values.T, items_uniq, item_user_dict)
pearson_corr_item = np.nan_to_num(pearson_corr_item)
item = 0
L = 20
# 유사도가 높은 상위 5개의 items
neighbors = get_similar_items(pearson_corr_item, item, L)
pred_items, pred_ratings = predict_rating_sim_item(pearson_corr_item, matrix.values.T, neighbors, 0)
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Sound of Music, The (1965)
Item 2: Erin Brockovich (2000)
Item 3: Airplane! (1980)
Item 4: James and the Giant Peach (1996)
Item 5: One Flew Over the Cuckoo's Nest (1975)
Item 6: My Fair Lady (1964)
Item 7: Gigi (1958)
Item 8: Big (1988)
Item 9: Snow White and the Seven Dwarfs (1937)
Item 10: Princess Bride, The (1987)
3. Jaccard Index = Jaccard Similarity
jaccard_mat_item = make_jaccard_matrix(items_uniq, item_user_dict)
jaccard_mat_item
>>
array([[1.00000000e+00, 1.03482099e-01, 1.48905109e-01, ...,
0.00000000e+00, 5.79710145e-04, 0.00000000e+00],
[1.03482099e-01, 1.00000000e+00, 1.36007828e-01, ...,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[1.48905109e-01, 1.36007828e-01, 1.00000000e+00, ...,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
...,
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
1.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[5.79710145e-04, 0.00000000e+00, 0.00000000e+00, ...,
0.00000000e+00, 1.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
item = 0
L = 20
# 유사도가 높은 상위 5개의 items
neighbors = get_similar_items(jaccard_mat_item, item, L)
pred_items, pred_ratings = predict_rating_sim_item(jaccard_mat_item, matrix.values.T, neighbors, 0)
K = 10
print_recommends(pred_items[0:K])
>>
Recommendations ==============================
Item 1: Tarzan (1999)
Item 2: Sound of Music, The (1965)
Item 3: James and the Giant Peach (1996)
Item 4: Gigi (1958)
Item 5: One Flew Over the Cuckoo's Nest (1975)
Item 6: My Fair Lady (1964)
Item 7: Wizard of Oz, The (1939)
Item 8: Christmas Story, A (1983)
Item 9: Big (1988)
Item 10: Ben-Hur (1959)
수학적으로는 쉬운 알고리즘이지만 구체적으로 코딩으로 구현할 때는 이것저것 신경쓸게 많은 알고리즘임을 알 수 있었다.
다음에는 Matrix Factorization과 BPR의구현을 포스팅할 예정이다.
References:
https://towardsdatascience.com/reshaping-a-pandas-dataframe-long-to-wide-and-vice-versa-517c7f0995ad
https://abluesnake.tistory.com/110
'Recommender Systems' 카테고리의 다른 글
| Basic Collaborative Filtering Models (0) | 2024.04.15 |
|---|---|
| Recommender Systems Papers (0) | 2024.02.22 |
| 추천 시스템 소개 (0) | 2024.01.31 |

