S4 논문의 제목은 Efficiently Modeling Long Sequences with Structured State Spaces다. (링크)
저자는 Albert Gu, Karan Goel, Christopher Ré다.
Gitub: 링크
Structured State Space Sequence Model이라 S4라고 불린다. 이번 논문에서도 역시나 Albert Gu가 쓴 논문이다.
제목에서부터 알 수 있듯이 HiPPO와 다르게 효율성에 중점을 둔 모델이다.
Abstract
시퀀스 모델링의 주된 목표는 단일한 원칙에 입각한 모델로 다양한 모달리티의 데이터를, 특히 long-range dependencies 장기 의존성을 가지는 데이터, 모델링하는 것이다. RNNs, CNNs 그리고 트랜스포머 모델들과 같은 전통적인 모델들은 장기 의존성을 잘 포착하는 specialized variants 특화된 변형들을 가지고 있음에도 불구하고, 여전히 10,000 이상의 스텝에 대한 굉장히 긴 시퀀스의 규모에 대해서는 어려움을 겪고있다. 시퀀스 모델링에 대한 최근의 유망한 모델은 근본적인 state space model (SSM) $x' (t) = Ax(t) + Bu(t), y(t) = Cx(t) + Du(t)$를 시뮬레이팅하여 state matrix A를 적절히 선택하여 수학적으로 그리고 실증적으로 장기 의존성을 다루는 방법을 제시한다. 하지만 이 방법은 엄두도 못낼 정도로 비싼 계산량과 메모리 요구량을 지니므로, 일반적인 시퀀스 모델링으로 실행하기는 거의 불가능하여 제시하기 어렵다. 저자들은 Structured State Space sequence model (S4)라는 SSM을 위한 새로운 parameterization 매개변수화 방법을 제시하고, 이론적인 강점을 가지면서도 기존의 방법에 비해 계산 효율적임을 보인다. 이 방법에는 low-rank correction을 통한 conditioning A를 포함하며, 안정적인 diagonalization 대각화와 잘 연구된 Cauchy kernel의 계산으로 SSM의 계산량을 줄인다. S4는 다양한 범위의 벤치마크에 대한 강력한 실증적 결과를 포함하는데 (i) 데이터 증강이나 auxiliary losses가 없이 sequential CIFAR-10에서의 91% accuracy 을 달성했으며 on par with a larger 2-D ResNet, 2-D ResNet과 동등한 결과를 달성했다. (ii) 이미지와 언어 모델링 태스크에 대한 트랜스포머 모델과의 굉장히 작은 차이를 지니면서도 60배 빠른 속도를 지닌다. (iii) Long Range Arena 벤치마크의 모든 태스크에 대해서 SoTA를 달성했는데, challenging Path-X task of length 16k라는 어려운 태스크를 포함하고 이는 다른 경쟁 모델들에 비해서 효율적이다.
2. Background: State Spaces
섹션 2.1 부터 2.4에서는 아래 Figure 1에서 제시된 SSM의 4가지 성질을 묘사한다. 이는 Classic continuous-time representation, LRDs를 다루는 HiPPO 프레임워크, discrete-time recurrent representation, parallelizable convolution representation이다. 섹션 2.4에서는 SSM convolution kernel인 $\overline{K}$를 소개하고 이에 대한 이론적 기여는 섹션 3의 초점이다.

2.1. State Space Models: A Continuous-time Latent State Model
State Space model은 (1)에서 제시된 간단한 식이다. 이는 1-D input signal $u(t)$를 N-D latent state $x(t)$로 매핑하며, 그다음 1-D output signal $y(t)$로 프로젝션한다.
$x' (t) = Ax(t) + Bu(t) $
$ y(t) = Cx(t) + Du(t)$ ... (1)
SSM은 Hidden Markov Models (HMM)과 같은 latent state models이나 다양한 과학 분야에서 널리 사용되고 있다. 저자들의 목표는 SSM을 이용해서 딥 시퀀스 모델의 black-box representation 블랙박스 표현으로의 사용이며, 이때 $A, B, C, D$의 파라미터들은 그라디언트 디센트로 학습한다. 본 논문의 남은 부분들에서 저자들은 파라미터 $D$를 생략하는데 (이는 $D = 0$으로 간주하는 것과 동치이며), 이는 $Du$가 skip connection으로 볼 수 있으며 따라서 쉽게 계산할 수 있기 때문이다.
2.2. Addressing Long-Range Dependencies with HiPPO
(1)에서 제시된 SSM은 간단하지만 실제로 적용하기는 어렵다. 직관적으로 하나의 설명은 exponential function을 풀기 위한 linear first-order ODEs는 시퀀스의 길이에 따라서 지수적으로 증가하는 그라디언트라는 문제점을 지닐 수 있다 (Vanishing / exploding gradients 문제). 이런 문제를 다루기 위해서 Linear State Space Layer (LSSL)dms HiPPO의 continuos-time memorization을 지렛대 삼아서 사용한다. HiPPO는 특정한 행렬들 $A \in \mathbb{R}^{N \times N}$의 클래스를 구체화하여 상태 $x(t)$가 입력 $u(t)$의 히스토리를 기억하도록 만든다. 예를 들어서 LSSL은 SSM은 임의의 행렬 $A$를 (2)의 형태로 간단히 수정해서 sequential MNIST 벤치마크의 성능을 60%에서 98%로 향상시켰다.
HiPPO Matrix
$$
\text{(HiPPO Matrix)} = A_{nk} =
\begin{cases}
(2n+1)^{1/2}(2k+1)^{1/2} & \,\,\, ,if \,\, n \gt k\\
n+1 & \,\, ,if \,\,\, n = k\\
0 & \,\, ,if \,\,\, n \lt k\\
\end{cases}
$$
n번째 row, k번째 column의 값을 위와 같이 정의한다.
보면 알겠지만 시간을 나타내는 첨자인 $t$가 없다.
2.3. Discrete-Time SSM: The Recurrent Representation
연속 함수 $u(t)$ 대신 discrete input sequence ($u_0, u_1, ...$)를 적용하기 위해서는 (1)을 step size $\Delta$로 이산화하며 이는 곧 입력의 resolution 해상도를 의미한다. 개념적으로 입력 $u_k$는 연속 신호 $u(t)$에 내재된 샘플링으로 볼 수 있다. 이때 $u_k = u(k \Delta)$다.
A method of analysing the behaviour of linear systems in terms of time series 논문의 방법대로 bilinear method를 이용하여 연속형 SSM을 이산화한다. State matrix $A$를 근사인 $\overline{A}$로 변환한다.
이산형 SSM은 식 (3)과 같다.
$x_k = \overline{A}x_{k-1} + \overline{B} u_k$
$y_k = \overline{C}x_{k}$
$\overline{A} = (I - \Delta/2 \cdot A)^{-1} (I + \Delta/2 \cdot A) $
$\overline{B} = (I - \Delta/2 \cdot A)^{-1} (\Delta B) $
$\overline{C} = C$ ... (3)
식 (3)은 이제 function-to-fuction이 아닌 sequence-to-sequence로 $u_k \rightarrow y_k$로 매핑한다.
$x_k$ 내에서 state equation은 recurrence이므로 SSM이 RNN처럼 계산 가능하도록 만든다. 구체적으로 $x_k \in \mathbb{R}^N$을 transition matrix $\overline{A}$를 가진 hidden state로 볼 수 있다.
본 논문에서 $\overline{A}, \overline{B}$은 이산화된 SSM 행렬들을 의미한다. 이 행렬들은 $A$와 step size $\Delta$의 함수다.
2.4. Training SSMs: The Convolutional Representation
Recurrent SSM (3)은 sequentiality 때문에 현재 하드웨어에서 학습하기 적합하지 않다. 대신 (1)과 같은 linear time-invariant (LTI) SSMs와 continuous convolutions 사이의 잘 알려진 연결은 존재한다. 이에 부합하도록 (3)은 discrete convolution으로 쓸 수 있다.
단순하게 하기 위해서 initial state $x_{-1} = 0$으로 설정한다.
$x_0 = \overline{B} u_0 \,\,\, x_1 = \overline{AB} u_0 \overline{B} u_1 \,\,\, x_2 = \overline{A}^2 \overline{B} u_0 + \overline{AB} u_1 + \overline{B} u_2 $
$y_0 = \overline{CB} u_0 \,\,\, y_1 = \overline{CAB} u_0 \overline{CB} u_1 \,\,\, y_2 = \overline{C}\overline{A}^2 \overline{B} u_0 + \overline{CAB} u_1 + \overline{CB} u_2 $
이는 (5) 형태의 컨볼루션 커널과 함께 (4)의 컨볼루션 형태로 벡터화할 수 있다.
$y_k = \overline{C}\overline{A}^k \overline{B} u_0 +\overline{C}\overline{A}^{k-1} \overline{B} u_1 + ... + \overline{CAB} u_{k-1} + \overline{CB} u_k$
$y = \overline{K} * u$ ... (4)
$\overline{K} \in \mathbb{R}^L := K_L( \overline{A}, \overline{B}, \overline{C} ) := (\overline{C}\overline{A}^i \overline{B} )_{i \in [L]} =(\overline{CB}, \overline{CAB}, ..., \overline{C}\overline{A}^{L-1} \overline{B}) $
다시 말해서, 식 (4)는 single (non-circular) 컨볼루션이고, $\overline{K} $가 알려져있다면 FFTs로 효율적으로 계산할 수 있다. 하지만 $\overline{K} $의 계산은 non-trivial이고 이에 대한 기술적 기여는 섹션 3에서 소개된다. 저자들은 $\overline{K} $을 SSM convolution filter 혹은 filter라고 부른다.
3. Method: Structured State Spaces (S4)
저자들의 기술적 결과는 S4의 parameterization와 섹션 2에서 소개된 다양한 SSMs; the continuous representation ($A, B, C$) (1), the recurrent representation ($\overline{A}, \overline{B}, \overline{C}$) (3), and the convolutional representation $\overline{K}$ (4)을 얼마나 효율적으로 계산할 수 있는지에 초점을 둔다.
섹션 3.1에서는 선형대수의 conjugation와 diagonalization의 개념에 근거하고 왜 이러한 접근법의 나이브한 응용이 작동하지 않는지를 논의한다. 섹션 3.2에서는 저자들이 제시한 고유의 방법의 개요를 소개하고 S4 parameterziation을 정의한다. 섹션 3.3에서는 주요 결과를 그리고 S4가 시퀀스 모델에 있어서 log factors만큼 점근적으로 효율적임을 보여준다. 증명은 Appendices B와 C에 나와있다.
3.1. Movitaion: Diagonalization
Discrete-time 이산시간 SSM (3)의 계산에서의 근본적인 병목은 $\overline{A}$에 의한 반복적인 행렬곱을 포함한다. 예를 들어서 (5)를 나이브하게 LSSL 방식으로 계산하면, $L$만큼의 연속적인 $\overline{A}$ 행렬곱을 수행하면 $O(N^2 L)$의 연산과 $O(NL)$의 공간이 필요하다.
Lemma 3.1. Conjugation은 SSMs에서 ($A, B, C$) ~ ($ V^{-1}AV, V^{-1}B, CV$)는 서로 equivalnce relation 동치 관계다.
따라서, $x' = Ax + Bu$와 $\tilde{x'} = V^{-1}AV $가 성립하며,
$y = Cx$와 $ y = CV \tilde{x}$가 성립한다.
Lemma 3.1은 행렬 $A$를 conjugation으로 canonical form으로 변환하고자 하는데, 이는 캐노니컬 폼이 보다 구조적이며 빠른 계산이 가능하기 때문이다. 예를 들어서 $A$가 diagonal이면 추적하기 쉬워진다. 특히, 목표로 하는 (4)의 $\overline{K}$는 이론적으로 $O((N + L) \log_2 (N + L))$의 산술 연산만을 필요로 하는 Vandermonde product이 될 수 있다.
안타깝게도, diagonalization를 단순히 적용하는 것은 numerical issues 수치적 문제로 인해 작동하지 않는다. (2)의 HiPPO 행렬에 명시적인 대각화를 유도해 보면, 그 원소들이 상태 크기 $N$에 대해 지수적으로 커진다는 사실을 알 수 있다. 대각화를 수치적으로 불가능하게 만든다. (예를 들어, Lemma 3.1의 $CV$는 계산이 불가능해 진다.) 저자들은 Combining recurrent, convolutional, and continuous-time models with the structured learnable linear state space layer 논문에서 naive한 알고리즘보다 $K$를 더 빠르게 계산하기 위한 다른 (구현되지 않은) 알고리즘을 제안한 바 있다. 하지만 Appendix B에서 증명했듯이, 이 알고리즘 또한 비슷한 이유로 수치적으로 불안정하다.
Lemma 3.2. 식 (2)의 HiPPO 행렬인 $A$는 행렬 $V_{ij} = \binom{i+j}{i-j}$에 의해 대각화된다. 특히, $V_{3i, i} = \binom{4i}{2i} \approx 2^{4i}$다. 따라서 $V$는 $2^{4N / 3}$까지 비례해서 커진다.
3.2. The S4 Parameterization: Normal Plus Low-Rank
이전 논의는 $V$와 같은 well-conditioned 행렬로만 conjugate해야 함을 시사한다. 가장 이상적인 시나리오는 행렬 $A$가 완벽하게 조건이 좋은 (Unitary) 행렬에 의해 diagonalizable 대각화 가능한 경우다. 선형대수의 Spectral Theorem에 따르면, 이는 정확히 normal matrices의 범주에 해당한다. 하지만 이러한 행렬 카테고리는 제한적이며, 특히 (2)의 HiPPO 행렬은 여기에 속하지 않는다.
% Spectral theorem은 행렬 $A$가 대각화 가능하다면 $A = PDP^{-1}$로 표기가 가능함을 의미한다. 이때 행렬 $D$는 diagonal matrix다.
행렬 $A$는 다음의 성질을 만족하면 Normal matrix다. Conjugate transpose of $A$를 $A*$ 혹은 $A^{H}$로 표기할 때, $AA* = A*A$다.
저자들은 HiPPO 행렬이 normal은 아니지만, normal matrix와 low-rank matrix의 합으로 분해될 수 있음을 관찰했다. 하지만 이것만으로는 여전히 유용하지 않다. 대각 행렬과 달리, 이러한 합을 powering 거듭제곱 연산 (식 (5) 참조)은 여전히 느리고 쉽게 최적화되지 않기 때문이다. 이러한 병목 현상을 극복하기 위해 세 가지 새로운 기법을 동시에 적용한다.
- $\overline{K}$를 직접 계산하는 대신, roots of unity 단위근 $\zeta$에서 truncated generating function {\sum_{를 평가하여 그 스펙트럼을 계산한다. $\overline{K}$는 inverse FFT**을 적용하여 찾을 수 있다.
- 이 생성 함수는 matrix resolvent와 밀접하게 관련되어 있으며, 이제 거듭제곱 대신 역행렬을 포함한다. 이제 low-rank term은 Woodbury identity을 적용하여 수정할 수 있으며, 이는 $(A + PQ*)^{-1}$를 $ 항으로 줄여, 진정한 대각 행렬 케이스로 만든다.
- 마지막으로, 대각 행렬이 Cauchy kernel $\frac{1}{\omega_j - \zeta_k}$의 계산과 동일함을 보인다. 이는 안정적인 near-linear algorhtims가 있는 잘 연구된 문제다.
이러한 기법들을 적용하여, 어떠한 행렬이든 Normal Plus Low-Rank (NPLR)로 분해할 수 있다.
Theorem 1. 모든 HiPPO 행렬들은 NPLR 표현을 갖는다.
$A = V \Lambda V* - PQ^\top = V(\Lambda - (V*P)(V*Q)*)V*$
이때, $V \in \mathbb{C}^{N \times N}$이고, $\Lambda$는 diagonal, $P, Q \in mathbb{R}^{N \times r}$은 low-rank factorization이다. 이러한 행렬들은 HiPPO-LegS, LegT, LagT과 r = 1이거나 2일 때 모두 만족한다. 식 (2)는 r = 1일때의 NPLR이다.
아래 Algorithm 1은 S4 Convolution Kernel의 계산 과정을 정리한 내용이다.

3.3. S4 Algorithms and Computational Complexity

L은 sequence length, B는 batch size, H는 hidden dimension을 의미한다.
4. Experiments
4.1. S4 Efficiency Benchmarks

Table 2와 3는 S4나 LSSL이나 다른 트랜스포머 구조에 비해서 얼마나 효율적인지를 보여준다.
4.2. Learning Long Range Dependencies
Long Range Arena (LRA)는 길이가 1K-16K steps인 6개의 태스크를 포함하는 벤치마크로 similarity, structural and visuospatial reasoning을 요구한다.
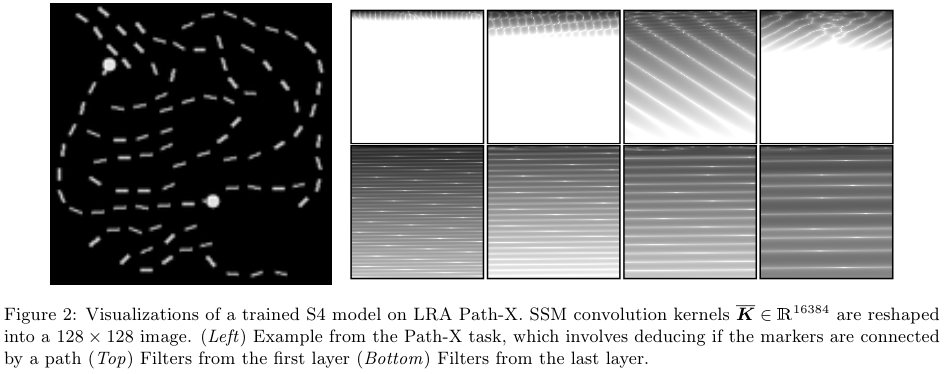
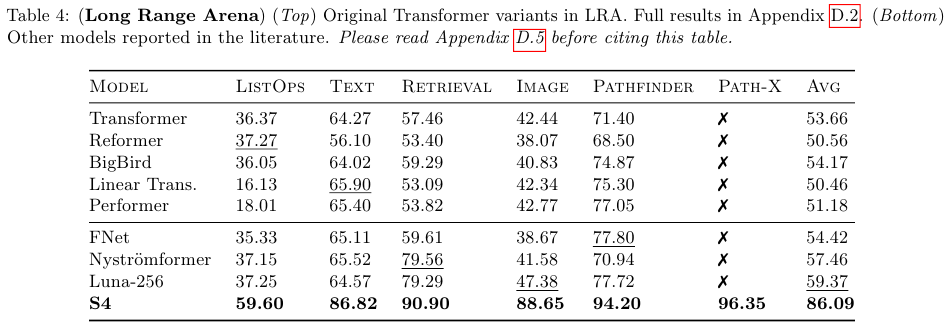
S4가 Transformer, BigBird 등의 다른 모델들 보다 더 좋은 성능임을 알 수 있다.
4.3. S4 as a General Sequence Model
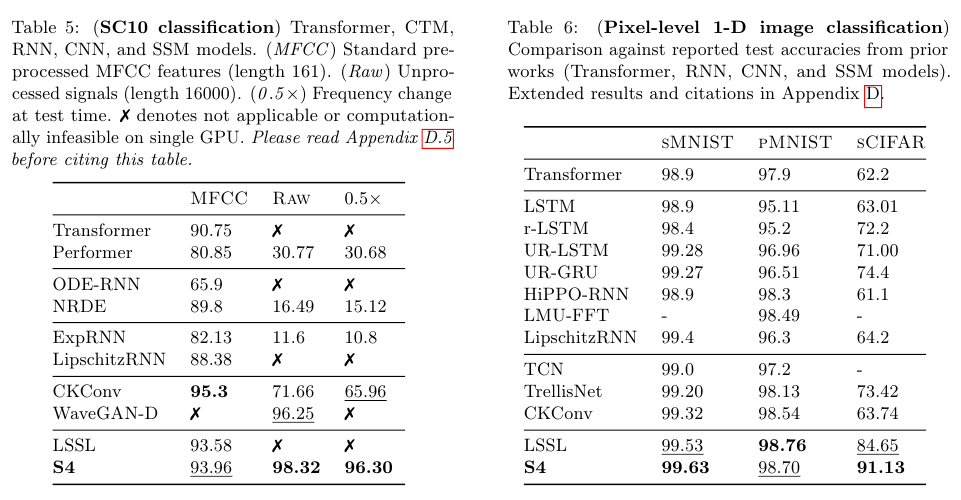
아래 Table 5에 제시된 SC10은 Raw Speech Classification을 다루는 signal 관련된 데이터에 대한 분류 성능 실험이다.
Table 6에 제시된 내용은 LRD의 pixel-level image classification에 대한 실험 결과다.
아래 Table 7은 CIFAR-10 데이터에 대한 실험으로 기존의 autoregressive models와는 다른 방식으로 이미지를 생성하는 실험이다.
Table 8은 Langauge modeling으로 컨텍스트에 기반한 생성 능력을 평가한다.

여담
논문에서 사용한 모든 증명이나 정리들을 완벽히 이해한건 아니지만,
여러가지 수학적 테크닉과 정리들로 HiPPO의 Long range depencies에 대한 장점을 보존하면서도 효율적인 행렬 계산을 달성하려는 목적 자체는 이해했다.
References:
https://en.wikipedia.org/wiki/Vandermonde_matrix
https://en.wikipedia.org/wiki/Spectral_theorem
https://en.wikipedia.org/wiki/Normal_matrix
'Time Series' 카테고리의 다른 글
| ARIMA와 ARCH 계열 모델들 정리 (0) | 2025.05.18 |
|---|---|
| HiPPO (2020) 논문 리뷰 (0) | 2025.05.17 |
| Wave 파동 기본 개념 정리 (0) | 2025.04.28 |
| Time Series Analysis 개요 (0) | 2025.04.23 |

