SSD의 논문의 제목은 SSD: Single Shot MultiBox Detector이다. (링크)
저자는 Wei Liu, Dragomir Anguelov, Dumitru Erhan, Christian Szegedy, Scott Reed, Cheng-Yang Fu, Alexander C. Berg다.
SSD 알고리즘은 논문 제목에서도 알 수 있듯이 object detection 문제를 푼다.
Abstract
SSD로 명명된 우리의 방법으로 서로 다른 aspect ratios와 scales를 가진 feature map location으로 부터 발생하는 default box를 이산화하여 bounding box (이하 bbox)를 만들고자 한다. 예측 국면에서 네트워크는 각각의 오브젝트 카테고리의 존재 가능성에 대한 score를 가진다. 해당 점수는 default box에 속해있으며 오브젝트의 모양에 맞도록 박스를 조정하게 된다. 추가적으로 네트워크는 다양한 해상도 resolution에서 나오는 multiple feature를 결합하여 예측을 하기 때문에 다양한 input image에 대응할 수 있다. SSD는 proposal 생성과 그에 따르는 픽셀 혹은 피쳐의 resampling을 제거하였으며 오로지 하나의 네트워크만을 사용한다. 따라서 SSD는 학습하고 다른 시스템과 통합하기 쉽다. PASCAL VOC, COCO, ILSVRC 데이터에 대해서 더 빠르면서도 비견될만한 성능을 보인다.
1. Introduction
SSD 논문의 contributions
- Single shot detector인 YOLO 보다 빠르며 Faster R-CNN만큼 정확하다.
- SSD는 작은 사이즈의 convolution 필터를 사용한 한정된 개수의 default bbox로 카테고리 별 점수를 예측한다.
- 서로 다른 스케일 (인풋 사이즈)에 대해서 좋은 성능을 낸다.
- 다른 알고리즘에 비해서 빠르다.
2. The Single Shot Detector (SSD)

Model
VGGNet의 베이스 네트워크에서 뒷 부분의 Fully Connected layer를 제외하고 feature만 사용한다.
베이스 네트워크 뒤에 여러개의 conv layers를 추가하고 여기서 생성되는 서로 다른 사이즈의 피쳐를 Detection layers로 보낸다.
추가된 레이어들을 Extra Feature Layers라고 한다.
이를 통해서 Multi-scale feature map을 구성한다.
각각의 Added feature layer는 고정된 detection prediction을 생성한다.
만약 한 feature layer의 size가 $m x n x p$, $p$는 채널 수인 경우 카테고리의 점수를 계산하거나 default box 좌표의 shape offeset을 생성한다.
개별 Feature map의 cell에서의 per-class score와 shape offset을 각각 계산한다.
개별 박스의 위치에서 나온 $k$개를 활용하여 $c$ class scores와 4 offsets relative to the original default box shape를 구하게 된다.
개별 location 근처에 $(c+4)k$ 필터가 존재하며 $m x n$ feature map에 대해서 $ (c+4)kmn $개의 outputs 도출된다.
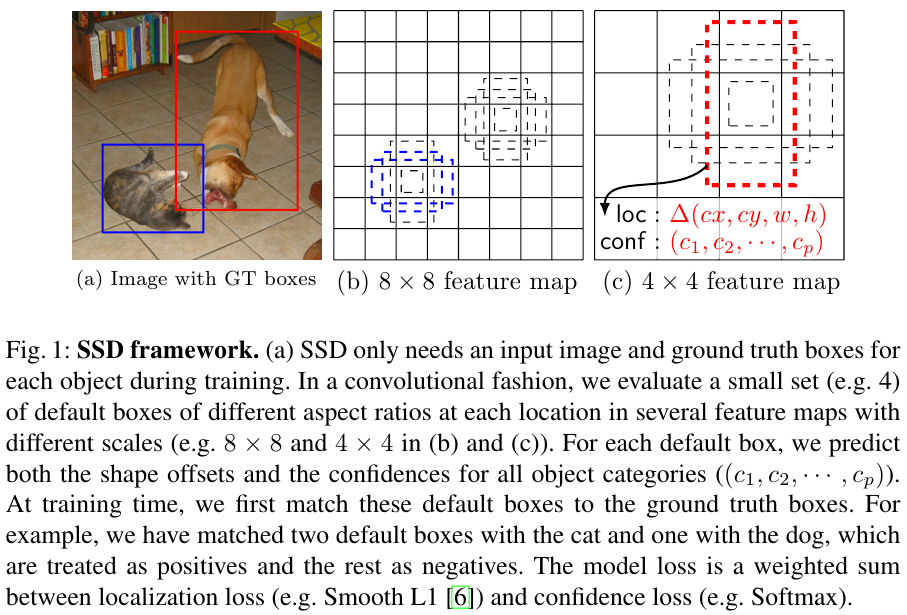
Training Objective
SSD의 학습 목표 함수는 MultiBox objective에서 유래한다.
$x_{ij}^{p}$ = {1, 0}은 카테고리는 $p$ 에 대해서 $i$-th default box와 $j$-th ground truth box가 서로 옳게 짝지어지는지 아닌지를 나타낸다.
$\sum_{i} x_{ij}^{p} \geq 1$이다.
최종 loss는 localization loss (loc)과 confidence loss (conf)의 weighted sum으로 구성된다.
$L(x, c, l, g) = \frac{1}{N} L_{conf}(x, c) + \alpha L_{loc}(x, l, g) $.
N은 matched feault box의 수다.
Bbox의 center $(cx, cy)$, default bbox는 $d$, default bbox의 width $w$, height는 $h$로 표기한다.
Localization loss는 $L_{loc}(x, l, g)= \sum_{i \in Pos}^{N} \sum_{m \in {cx, cy, w, h}} x_{ij}^{k} \operatorname{smooth}_{L1} ( l_i^{m} - {\hat{g}}_j^{m} ) $
where
$ {\hat{g}}_j^{cx} = (g_j^{cx} - d_i^{cx}) / d_i^{w}$
${\hat{g}}_j^{cy} = (g_j^{cy} - d_i^{cy}) / d_i^{h}$
${\hat{g}}_j^{w} = log \frac{ g_j^{w} }{ d_i^{w} } $
${\hat{g}}_j^{h} = log \frac{g_j^{h} }{d_i^{h} } $
그리고 confidence loss는 아래와 같이 정의된다.
$ L_{conf}(x, c) = - \sum_{i \in Pos}^{N} x_{ij}^{p} log({\hat{c}}_i^{p} ) -\sum_{i \in Neg} log({\hat{c}}_i^{0}) $
where
$log( {\hat{c}}_i^{p} = \frac{exp(c_i^{p})}{ \sum_p exp(c_i^{p} }$
Weight term인 $\alpha$는 cross validation에 의해서 1로 설정했다.
Choosing scales and aspect ratios for default boxes
여러개의 feature map에 따라서 default boxes의 스케일은 아래와 같이 계산한다.
$s_{min}$은 0.2, $s_{max}$은 0.9으로 계산한다. 이는 Lowest layer의 스케일은 0.2, higest layer는 0.9의 스케일을 갖는다.

Hard negative mining
모든 negatives를 사용하는데 아니라 각 default box에 대해 higest confidences loss를 negatives를 선정해서 사용했다.
Negatives : Positives의 비율이 3:1이 되도록 조정한다.
Data augmentation
다양한 인풋 사이즈에 Robust하게 만들기 위해서 다음의 옵션들 중에서 하나를 사용했다.
- Entire original input image
- Sample a patch that has minimum jaccard overlap with the object with in {0.1, 0.3, 0.5, 0.7, 0.9}
- Randomly sample a patch
Sampled patch의 사이즈는 오리지널 사이즈의 [0.1, 1]의 사이즈를 사용하였으며 aspect ratio는 1/2과 2사이다.
3. Experimental Results
Fast는 Fast R-CNN, Faster는 Faster R-CNN을 의미한다.

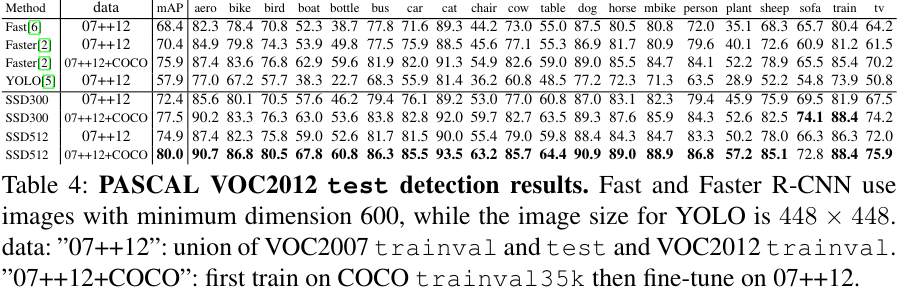
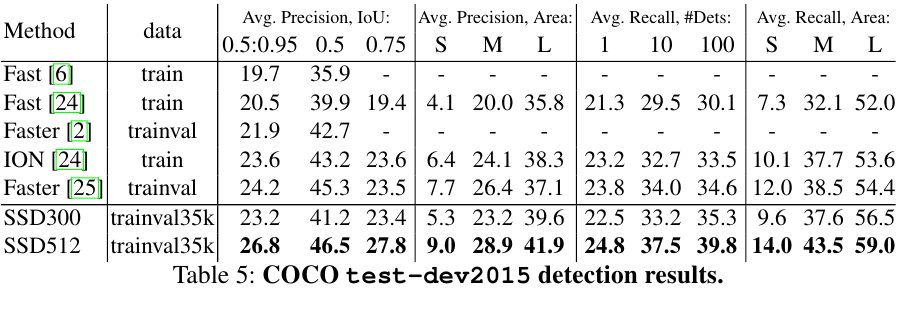
Table 1, 4, 5를 보면 SSD가 대체로 좋은 성능을 보인다.

References:
'Computer Vision' 카테고리의 다른 글
| FaceNet (2015) 논문 리뷰 (0) | 2025.04.07 |
|---|---|
| DenseNet (2017) 논문 리뷰 (0) | 2025.04.07 |
| CAM (2015) 논문 리뷰 (0) | 2025.04.07 |
| YOLO v1 (2015) 논문 리뷰 (0) | 2025.04.06 |
| U-net (2015) 논문 리뷰 (1) | 2025.04.06 |



