GLU variants가 나온 의 논문 이름은 GLU Variants Improve Transformer다. (링크)
저자는 Noam Shazeer다.
GLU는 Gated Linear Units의 약자다.
Abstract
GLU, Gated Linear Units은 두 개의 linear projections의 component-wise product로 구성된다. 여기서는 다양한 GLU의 variants를 탐구한다. ReLU와 GELU 보다 좋은 성능임을 보인다.
Introduction
Transformer 베이스의 모델들의 내부의 Position-wise Feed-Forward Networks (FFN)에서 activation 함수들이 쓰인다.
T5에서는 bias가 없는 버젼이다.
ReLU는 $\text{FFN}_\text{ReLU}(x, W_1, W_2) = \text{max}(xW_1, 0)W_2$로 표시할 수 있다.
GELU의 경우 $\text{FFN}_\text{GELU}(x, W_1, W_2) = \text{GELU}(xW_1)W_2$로,
$\text{Swish}_{\beta}(x)$의 경우 $\text{FFN}_\text{Swish}_{1}(x, W_1, W_2) = \text{ Swish }_{1}(xW_1)W_2$로 표기한다.
GELU는 Gaussian Error Linear Units로 GELU($x$) = $x \Phi{x}$다. 이때 $\Phi$는 CDF of normal distribution이다.
$\text{Swish}_{\beta}(x) = x \sigma(\beta x)$ 함수다. $\sigma$는 sigmoid 함수다.
Gated Linear Units (GLU) and Variants
GLU$(x, W, V, b, c) = \sigma(xW + b) \otimes (xV + c) $
Bilinear$(x, W, V, b, c) = (xW + b) \otimes (xV + c) $
이때 $\otimes$는 component-wise product = element-wise product = Hadamard product다.
ReGLU$(x, W, V, b, c) = max(0, xW + b) \otimes (xV + c) $
GEGLU $(x, W, V, b, c) = GELU(xW + b) \otimes (xV + c) $
SwiGLU $(x, W, V, b, c, \beta) = \text{Swish}_{\beta}(xW + b) \otimes (xV + c) $
Bias term을 생략한 FFN과 activation은 아래와 같이 표기 가능하다.
$\text{FFN}_\text{GLU}(x, W, V, W_2) = (\sigma(xW) \otimes xV) W_2$
$\text{FFN}_\text{Bilinear}(x, W, V, W_2) = (xW \otimes xV) W_2$
$\text{FFN}_\text{ReGLU}(x, W, V, W_2) = (max(0, xW) \otimes xV )W_2$
$\text{FFN}_\text{GEGLU}(x, W, V, W_2) = (\text{GELU}(xW)\otimes xV)W_2$
$\text{FFN}_\text{SwiGLU}(x, W, V, W_2) = (\text{Swish}_{1}(xW)\otimes xV)W_2$
3. Experiments with T5
T5 base 220M 짜리 모델을 이용해서 실험했다.
Heldout-set log perplexity를 segment-filling tasks의 측면에서 측정했다.
3.2. Pre-training

GEGLU와 SwiGLU의 성능이 준수하다.
3.3. Fine-tuning
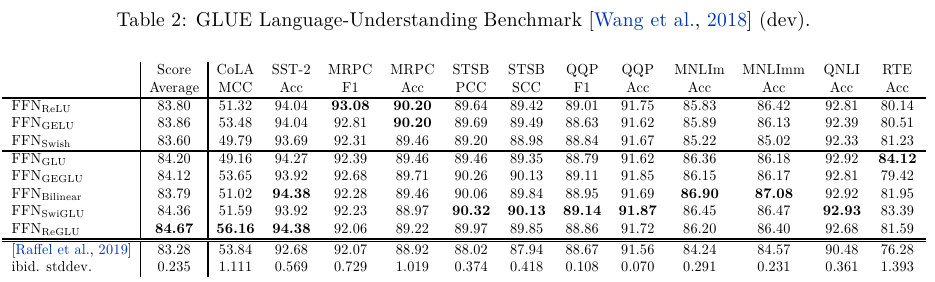
Bilinear, ReGLU, SwiGLU가 주목할만한 성능을 보여준다.
'NLP' 카테고리의 다른 글
| Tokenizer 간단하게 정리 (0) | 2025.04.15 |
|---|---|
| Longformer (2020) 논문 리뷰 (0) | 2025.04.09 |
| MQA (Multi-Query Attention) (2019) 논문 리뷰 (0) | 2025.04.09 |
| GPT 2 (2019) 논문 리뷰 (0) | 2025.04.09 |
| Sentence-BERT (2019) 논문 리뷰 (0) | 2025.04.09 |

