LoRA의 논문 이름은 LoRA: Low-Rank Adaptation of Large Language Models다. (링크)
저자는 Edward J. Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, Weizhu Chen다.
Github: 링크
이름에서 알 수 있듯이 기존의 adapter 레이어를 추가하는 방식과 같지만 이를 low-rank로 만든다는 점에서 차이가 있다.
여기서 말하는 rank는 선형대수의 그 rank가 맞다.
Abstract
GPT-3 175B와 같은 큰 모델의 파인 튜닝은 매우 비싸다. 따라서 저자들은 Low-Rank Adaptation, LoRA를 제시한다.
모델의 원래 weigths를 프리즈하고 trainable rank decomposition matrices를 추가하는 구조다.
RoBERTa, DeBERTa, GPT-2 그리고 GPT-3에 대해서 파인튜닝한 퀄리티를 비교한다.
다른 adapters와는 다르게 addtional inference latency 추가적인 추론 레이턴시가 없다.
2. Problem Statement
Full fine-tuning의 최적화 과정은 아래 식과 같다.
$ \underset{\Phi}{\operatorname{max}} \sum_{(x, y) \in Z } \sum_{t = 1}^{|y|} log( P_{\Phi} ( y_t | x, y_{<t}) )$
pre-trained weights $\Phi_0$을 $\Phi_0 + \Delta \Phi$로 업데이트 한다.
이때 $|\Delta \Phi_0|$ = $| \Phi_0|$ 이므로 많은 양의 파라미터를 업데이트 해야 한다.
하지만 LoRA 논문에서 제시한 parameter-efficient 방법의 파라미터 증가분 $\Delta \Phi_0$ = $\Delta \Phi (\Theta) $다.
이때 $\Theta$는 훨씬 작은 크기의 파라미터다. $|\Theta|$ << $|\Phi_0|$.
따라서 보다 파라미터-효율적인 최적화 식은 아래와 같다.
$ \underset{\Theta}{\operatorname{max}} \sum_{(x, y) \in Z } \sum_{t = 1}^{|y|} log( p_{\Phi_0 + \Delta \Phi(\Theta) } ( y_t | x, y_{<t}) ) $
GPT-3의 175 B인 $|\Phi_0|$와 비교할 때 $|\Theta|$는 $|\Phi_0|$의 0.01%에 불과한 작은 크기다.
4. Our Method
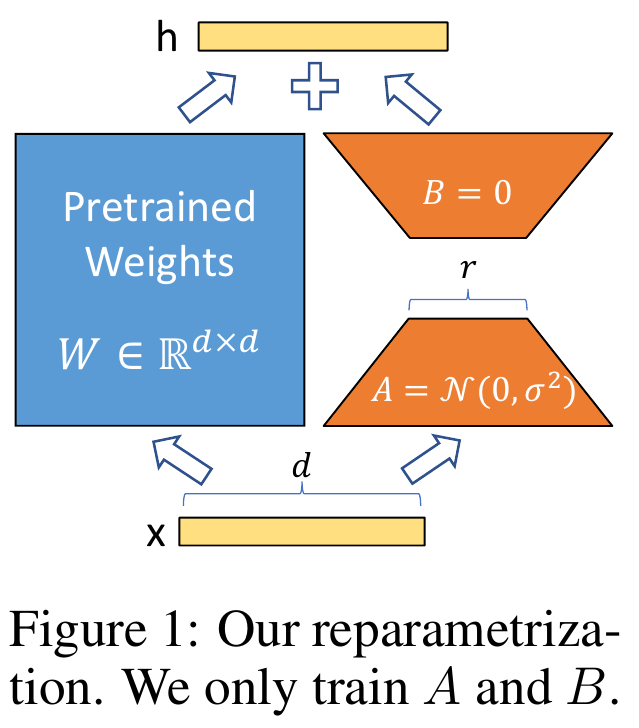
본래의 forward path인 $h = W_0 x$를 adapter layer를 적용한 modified forward path는 아래와 같다.
$h = W_0 x + \Delta W x = W_0 x + B A x$.
이때, Weight matrix $W_0 \in {\mathbb{R}}^{d \times k}, B \ in {\mathbb{R}}^{d \times r}, A \in {\mathbb{R}}^{r \times k} $ 이며, $r$ << min($d, k$)다.
$A$에 대해서는 random Gaussian initialization을 수행하고 $B$는 0으로 초기화 한다. 따라서 $\Delta W = BA$는 학습 초기에는 0이다.
5. Empirical Experiments
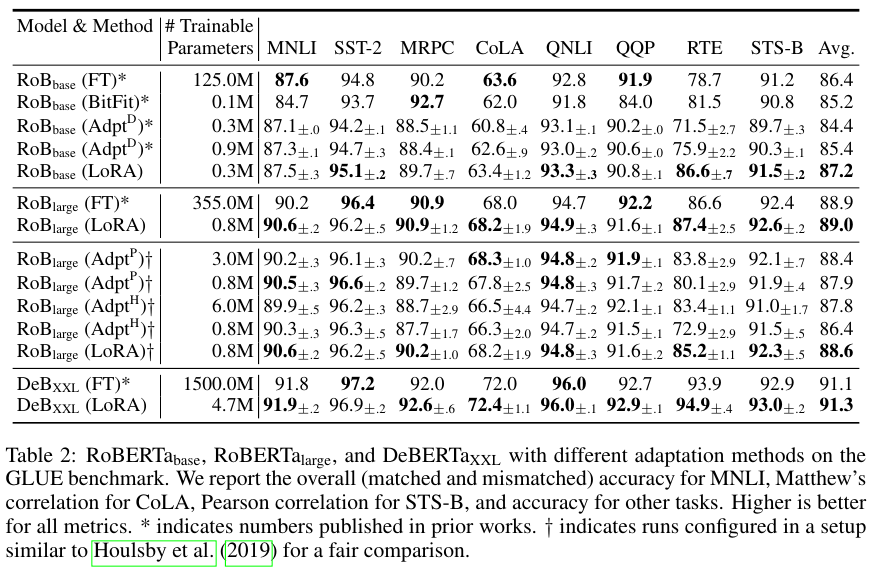

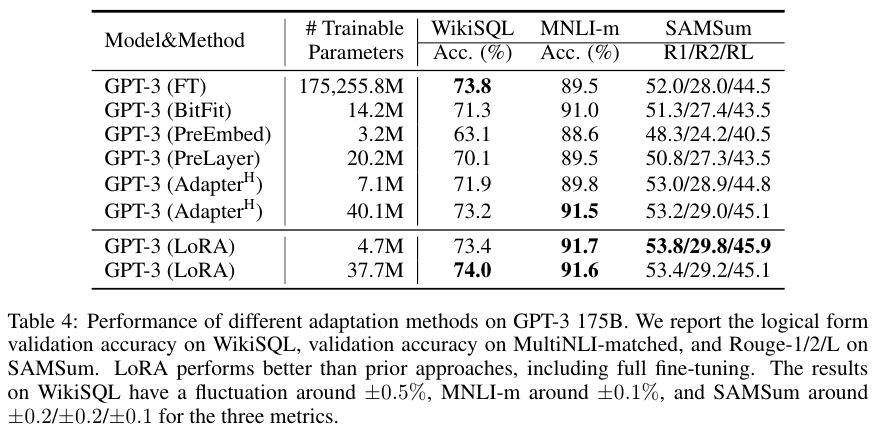
RoBERTa, DeBERTa, GPT-2, GPT-3에 대해서 다른 파인 튜닝 방법들과 비교한 결과 LoRA가 훨씬 적은 수의 파라미터로도 대체로 좋은 성능을 달성했음을 알 수 있다.
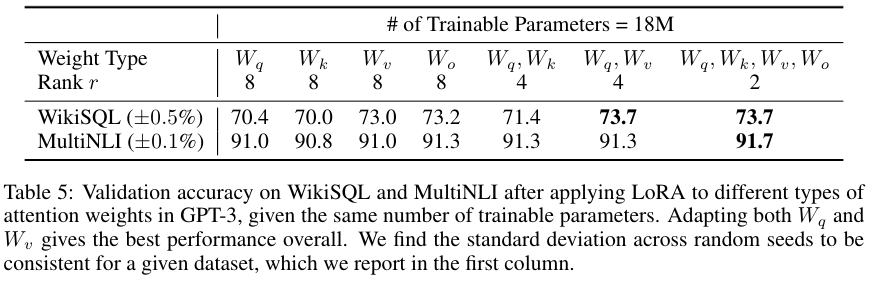
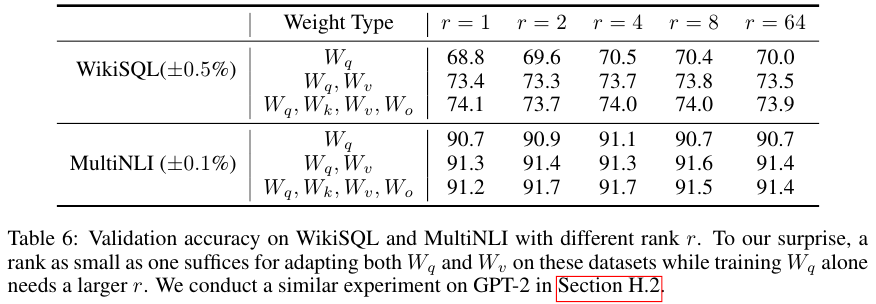
Table 5와 6은 Transformer 구조에서 어떤 레이어에 LoRA를 적용할 때 성능이 가장 좋은지, 그리고 low rank를 결정하는 $r$이 얼마나 작아야 하는지를 나타낸 표다.
$q, k, v, o$ 모두에 LoRA를 적용한다면 $r$이 무려 1이어도 좋은 성능을 달성함을 알 수 있다.
Appendix
LoRA의 하이퍼 파라미터에 대한 configs를 추가한다.
DeBERTa XXL

위 Table 10은 DeBERTa XXL을 GLUE에 적용할 때로, Optimizer는 AdamW, Warmup Ratio는 0.1, LR Schedule은 Linear인게 공통이다.
그외에 batch size, epochs, learning rate, weight decay, CLS dropout, LoRA config인 r과 적용 파라미터 종류, max sequence length는 모두 다르다. 대신 LoRA $\alpha$는 모두 8로 동일하다.
GPT-2

Table 11은 GPT-2에 LoRA는 적용하는데 E2E와 WebNLG, DART에 적용한다.
옵티마이저가 AdamW, Learninr Rate Schedule가 Linear, lr이 0.0002, batch size가 8, epoch가 5, LoRA 알파가 32로 공통적이다. Warmup Steps는 500이다.
모든 GPT-2에 대해 적용했다는거 보면 GPT-2 M과 L 모두에 동일한 설정을 적용한듯 싶다.
GPT-3
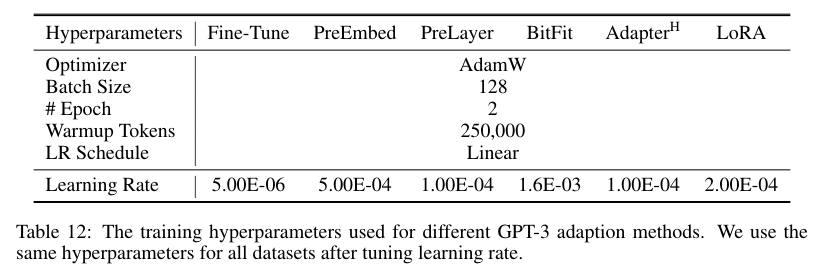
Table 12는 GPT-3에 적용한 서로 다른 adaption 방법에 대해서 어떻게 하이퍼 파라미터를 적용했는지에 대해서 나온다.
옵티마이저가 AdamW, Learninr Rate Schedule가 Linear, batch size가 128, epoch가 2, Warmup Steps는 250,000이다.
References:
https://asidefine.tistory.com/309
https://minyoungxi.tistory.com/116
https://pytorch.org/torchtune/0.4/tutorials/lora_finetune.html
https://github.com/huggingface/peft/blob/main/src/peft/tuners/lora/model.py
'NLP > LLM' 카테고리의 다른 글
| PaLM (2022) 논문 리뷰 (0) | 2025.04.11 |
|---|---|
| Scaling Laws for Neural Language Models (2020) 논문 리뷰 (0) | 2025.04.11 |
| OPT (2022) 논문 리뷰 (0) | 2025.04.11 |
| GPT 3 (2020) 논문 리뷰 (5) | 2025.04.09 |
| Small Language Models: Survey, Measurements, and Insights (0) | 2025.03.17 |



