Tree-of-Thought (ToT) 의 논문 제목은 Tree of Thoughts: Deliberate Problem Solving with Large Language Models이다. (링크)
저자는 Shunyu Yao, Dian Yu, Jeffrey Zhao, Izhak Shafran, Thomas L. Griffiths, Yuan Cao, Karthik Narasimhan다.
Github: 링크
Chain of Thought를 대신할 problem solving 구조를 제시한 논문이다.
Abstract
언어 모델은 광범위한 범위에 대해서 general problem solving 일반적인 문제 해결에 쓰이고 있지만 여전히 추론 과정에서 token-level과 left-to-right 의사 결정에 국한되어 있다. Exploration, strategic lookahead, initial decisions 탐색, 전략적 예측 또는 초기 결정에서 중요한 역할을 맡기에는 아직 부족함을 의미한다. 이를 surmount 극복하기 위해서 저자들은 Tree of Thoughts (ToT)라는 새로운 프레임 워크를 제시하는데, 이는 Chain of Thought를 일반화하여 문제 해결을 위한 중간 단계에서의 연속적인 텍스트의 유닛 (thoughts)의 탐색을 가능하게 한다. ToT는 언어모델로 하여금 deliberate 계획적인 의사 결정을 가능하게 하는데 이는 다양한 추론 경로에 대해서 고려하고 자기 평가 선택을 통해서 다음 행동의 경로를 결정할 뿐만 아니라 예측과 백트래킹 또한 같이 하면서 global choices를 필요하다면 수행하기 때문이다. Game of 24, Creative Writing, Mini Crosswords에서 유의미한 성과를 거두었다.
1. Introduction
Human cognition에서 사람은 dual process models를 가지고 결정을 내린다. 첫 번째는 fast, automatic, unconscious mode 빠르고 자동적이며 무의식적인 모드인 "Systems 1"이다. 두 번째는 slow, deliberate, consious mode느리고, 신중하며, 의식적인 모드인 "System 2"다. 강화학습에서는 "model free" learning과 보다 delibertae인 "model based" planning을 섞어서 사용한다. 간간단한 token-level choice의 경우 LM으로 하여금 System 1을 연상시킨다. 따라서 보다 deliberate인 System 2로 planning process를 도입하여 이용해 증강할 수 있다. 이는 System 2로 하여금 현재 선택에서 보다 다양한 대안들의 탐색을 가능하게 하고, 현재 상태를 평가하며 미래를 예측하고 이전의 결정들을 백트래킹하며 더 많은 글로벌 결정을 할 수 있다.
Newell, Shaw and Simon이 1950년대에 시작했던 problem solving 문제 해결을 특징지었는데 바로, tree 트리로 표현되는 combinatorial problem space에서의 search 탐색 문제로 보았다. ToT에서는 이를 사용해서 문제를 푼다.
다음의 Figure 1에서 ToT와 다른 방법들의 구조를 비교한다.
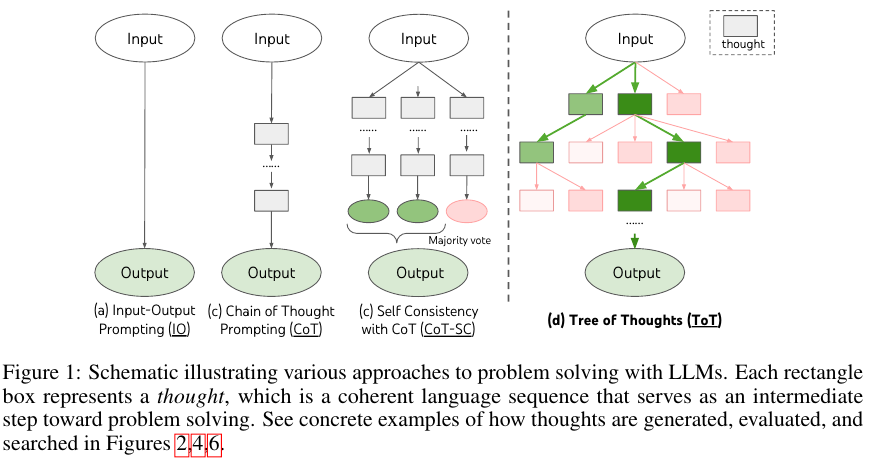
ToT는 개별 thought를 coherent language sequence로 간주하여 문제 해결을 위한 intermediate step 중간 단계으로 활용한다.
아래 Table 1과 같이 중간 단계로 활용한다.

2. Background
우선 언어 모델의 문제 해결에 대한 현재 방법들을 수식화한다.
파라미터 $\theta$를 갖는 사전 학습된 언어모델 LM을 $p_\theta$로 표시하며, 소문자들 $x, y, z, s, ... $은 language sequence 언어 문장 ($x$[1], ..., $x$[n])을 의미한다. 이때 각각의 $x$[$i$]는 token이다.
따라서 $p_\theta = \prod_{i=1}^n( x \left[ i \right] | x \left[ 1, ..., i \right] )$로 나타낼 수 있다.
대문자 $S$는 언어 문장의 collection이다.
Intput-Output (IO Prompting)
입력 $x$에 대한 출력 $y$를 이용하는 가장 흔한 형태의 방법이다.
LM: $y$ ~ $ p_\theta (y | \text{prompt}_{\text{IO} (x) }) $
이때 $\text{prompt}_{\text{IO}}$는 입력 $x$를 감싸면서 task instruction이나 few-shot input-output 예시들을 포함한다.
간단하게 표한하기 위해서
$p_\theta ( \text{output} | \text{prompt (input)} )$ 으로 표현하며,
$y$ ~ $ p_\theta^{IO} (y | x) $로 표현한다.
Chain-of-Thought (CoT) prompting
핵심 아이디어는 a chain of thoughs $z_1, ..., z_n$이 입력 $x$와 $y$를 연결한다.
각각의 $z_i$는 coherent language sequence로 문제 해결을 향한 의미있는 중간 단계다.
개별 $z_i$는 sampled seuquentially 순차적으로 샘플링 된다.
$z_i$ ~ $ p_\theta^{CoT} (z_i | x, z_{1, .., i - 1} ) $.
$y$ ~ $ p_\theta^{CoT} (y | x, z_{1, .., n}) $
실전에서는 [$z_{1, .., n}, y$] ~ $p_\theta^{CoT} (z_{1, .., n}, y | x) $의 형식으로 연속적인 언어 문장이 샘플링 된다.
따라서 decomposition of thoughts 생각의 분해는 왼쪽 방향에 대해서 ambiguous 애매모호하다.
Self-Consistency with CoT (CoT-SC)
CoT-SC는 앙상블 방법으로 $k$개의 CoT들, [$z_{1, .., n}^{(i)}, y^{(i)}$] ~ $p_\theta^{CoT} (z_{1, .., n}, y | x) $ ($i$ = 1, ..., $k$), 생성하고 가장 자주 등장하는 출력, $\text{argmax}_{y} \# \{ i | y^{ (i) } = y \} $ , 최종 답변으로 삼는 방법이다.
CoT-SC 역시 기본적인 CoT 방법을 사용했기 때문에 같은 문제를 지닌다.
3. Tree of Thoughts: Deliberate Problem Solving with LM
ToT는 문제를 트리에 대한 탐색으로 틀을 만들기 때문에 다음의 정의와 과정이 필요하다.
우선 개별 node 노드는 state 상태로서 $s = \left[ x, z_{1, ..., i} \right]$로 표기하며 입력 $x$와 현재까지의 thought 생각을 활용한 partial solution이다. ToT는 다음의 4가지 질문을 포함한다.
1. 중간 단계를 어떻게 생각의 단계로 분해할 것인가?
2. 각각의 상태에서 어떻게 잠재적인 생각을 생성할것인가?
3. 어떻게 상태를 휴리스틱하게 평가할것인가?
4. 어떤 탐색 알고리즘을 쓸것인가?
1. Thought Decomposition
CoT가 직접적인 생각의 분해가 없는 것과 달리 ToT에서는 문제의 properties 특성에 맞게 디자인하여 중간 생각 단계로 분해한다.

위 Table 1에서처럼 5x5 Crosswords의 경우 몇개의 단어들로, Game of 24의 경우는 한 줄의 방정식으로, Creative Writing에서는 글쓰기 계획의 전체 단락으로 구성된다. 일반적으로 생각은 LM이 promising and diverse samples를 생성할만큼 작아야 한다.
하지만 너무 작아서는 안되고 평가할 수 있을만큼 커야 한다. 책 한 권은 너무 크고, 토큰 하나는 너무 작다.
2. Thought Generator $G(p_\theta, s, k)$
트리 상태 $s = \left[ x, z_{1, ..., i} \right]$가 주어졌을 때 두 가지 전략을 통해서 $k$개의 후보를 생성하여 다음 생각 단계를 진행한다.
(a) Sample:
i.i.d thoughts from CoT prompt.
$z^j$~ $p_\theta^{CoT} (z_{i + 1} | s)$ = $p_\theta^{CoT} (z_{i + 1} | x, z_{1, ..., i} ) $ 그리고 $j = 1, ..., k$다.
이 방법은 thought space가 rich (e.g. each thought is paragraph)할때 잘 작동한다. i.i.d 샘플은 다양성을 유도한다.
Figure 4의 Creative Writing이 예시다.

(b) Propose
propose prompt를 이용해서 sequentially 연속적으로 생성한다.
[$z^{(1)}, ..., z^{(k)}$] ~ $p_\theta^{propose} (z_{i+1}^{(1, .., k)} | s) $.
이 방법은 thought space가 보다 constrained 제한적인 경우 (e.g. each though is just a word or a line) 더 잘 작동한다.
따라서 proposing은 같은 컨텍스트에 있는 서로 다른 생각의 중복을 피하게 해준다.
Figure 2의 Game of 24와 Figure 6의 Crosswords가 이에 속한다.
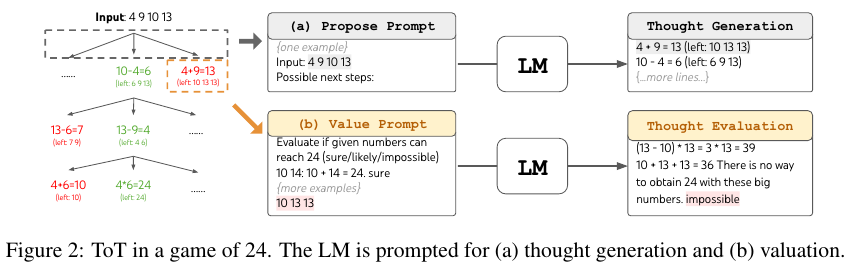

3. State Evaluator $V(p_\theta, S)$
서로 다른 상태의 frontier 경계에서 상태 평가자는 문제 해결을 향한 progress 진행을 평가한다. 이때 휴리스틱한 상태로 작동하기 때문에 탐색 알고리즘으로 하여금 어떤 상태에 대해서 어떤 순서로 탐색할지를 결정한다.
탐색 알고리즘의 경우 DeepBlue처럼 프로그램되어 있거나 AlphaGo처럼 학습할 수 있다.
반면 저자들은 세 번째 다른 방법인 휴리스틱 방법을 제시한다. 이는 프로그래밍 규칙 방법 보다는 유연하며 학습 모델의 방법 보다는 sample-efficient다. 다음 두 가지 전략을 제시하는데 각각을 독립적으로 사용할 수도 있고 함께 사용할 수도 있다.
(a) Value:
각각의 상태를 독립적이며, $V(p_\theta, S)(s)$ ~ $p_\theta^{value} (v| s) \, \forall s \, \in S$.
Value prompt는 상태 $s$에 대해서 스칼라 값 $v$ (가령 1부터 10)를 주거나 classification (e.g. sure/likely/impossible)의 형태로 평가하게 된다. 평가의 기반은 문제마다 생각의 단계마다 다르다. 저자들의 경우 explore evaluation에서는 몇개의 "lookahead 시뮬레이션"에 대해서 상태를 "good"과 "bad"로 평가했다. 평가는 완벽할 필요가 없으며 단지 의사 결정에 도움이 되면 된다.
(b) Vote:
$V(p_\theta, S)(s)$ = $\mathbb{I}[s = s*]$. ($\mathbb{I}$는 indicator function으로 마찬가지로 1을 mathbb 형태로 표기할 수 없어서 표기법을 변경했다.) 이때 "good" state $s*$ ~ $p_\theta^{vote} (s* | S) $는 서로 다른 상태들 사이에서 신중하게 비교되어 선택되며 이는 vote prompt에 의해 실행된다. Passage coherency 같이 직접적으로 가치를 매기기 어려울 때 다른 partial solutions를 서로 비교하는 대안이 가능하다.
두 개의 전략 모두 LM으로 하여금 여러번 value와 votes의 결과에 대해서 종합하도록 요청할 수 있다.
단시 time / resource / cost 와 faithful / robust 휴리스틱 사이의 트레이드 오프만을 기억하면 된다.
4. Search Algorithm
최종적으로 트리 구조에 맞춰서 어떤 답이 가장 좋은지 순회하며 알아보면 된다.
알고리즘 테스트를 공부하며 빈번하게 보면 BFS와 DFS가 등장한다.

(a) Breadth-first search (BFS)
Most promising states 를 매 스텝마다 $b$개 만큼 유지하도록 한다.
Game of 24와 Creative Writing에서는 트리의 depth 깊이를 3으로 제한한다. $T \leq 3$.
초기 생각 스텝은 평가된 다음에 더 작은 집합으로 pruned 된다 ($b \leq 5$).
(b) Depth-first search (DFS)
Most promising state를 맨 처음 찾으며 최종 출력에 닿을 때 까지 진행한다. ($t \gt T$).
혹은 상태 평가자가 현재 상태 s($V(p_\theta, \{ s \}) (s)$ $\leq v_{th}$ ($v_{th}$는 value threshold)에서 문제 해결이 불가능해 보일 때 까지.
후자의 경우 $s$로 부터 시작되는 subtree 서브트리는 pruned 되어 exploration을 exploitation에 대해서 거래한다.
양쪽의 케이스에 대해서 DFS는 $s$의 부모 상태에 대해서 백트래킹을 수행하며 탐색을 계속한다.
4. Experiments
Game of 24
+, -, *, / 의 네 가지 사칙연산으로 24를 만드는 게임이다.

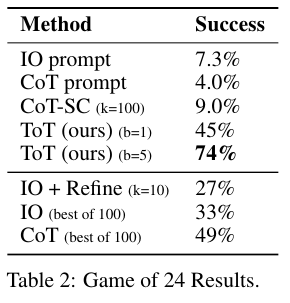

Figure 3에 나온대로 생각을 3단계로 쪼갰다. Propose prompt와 BFS와 $b$ = 5로 가장 좋은 결과를 얻었다.
평가의 경우 sure/maybe/impossible로 평가했다.
값들을 생각 마다 3번씩 샘플링했다.
IO와 CoT, CoT-SC가 10%도 안되는데 ToT는 최대 74%의 성공률을 보여주는걸 알 수 있다.
제일 놀라운 결과다.
Creative Writing
4개의 랜덤 문장이 입력으로 주어지고 각각에 대해서 coferent passage 이어지는 단락을 4개의 문장 각각에 맞게 작성하는 문제다.
하이 레벨의 계획과 창의적인 생각을 요하는 문제다.

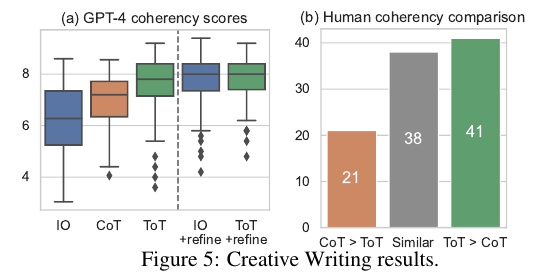
5개의 plans에서 voting을 5번 한 결과가 가장 좋았다. Depth는 2로 설정했으며 zero-shot vote prompt를 수행했으며 보팅은 매 단계마다 5번씩 샘플링했다. 그리고 breadth limit $b$ = 1로 설정해서 매 단계마다 하나씩만 그대로 가지고 있었다.
Mini Crosswords
5x5 크로스워드 문제다. IO 프롬프트와 CoT 프롬프트를 사용했으며 10 번을 샘플랑하고 평균낸 결과를 사용했다.
DFS를 사용하였다.
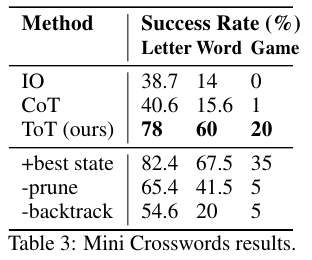

IO나 COT에 비해서 가장 좋은 성능임을 알 수 있다.
여담
프롬프트 엔지니어링쪽이 다 그렇겠지만 ToT는 생각 생성, 상태 평가, 탐색 방법까지 달라서 실무에서 유의미하게 쓰려면 이런저런 실험을 굉장히 많이 해봐야겠단 생각이다.
'NLP > Prompt & Problem Solving' 카테고리의 다른 글
| Prompt 관련 자료 모음 (0) | 2025.04.28 |
|---|---|
| ChartInstruct (2024) 논문 리뷰 (0) | 2025.04.27 |
| Lost in the Middle (2023) 논문 리뷰 (1) | 2025.04.27 |
| Plan and Solve (2023) 논문 리뷰 (1) | 2025.04.19 |
| CoT-SC (2022) 논문 리뷰 (0) | 2025.04.18 |


