Modern Portfolio Theory (MPT) 현대 포트폴리오 이론의 기본을 정리하고자 한다.
여기서 말하는 기본은 역시나 학부나 영문 Wikipedia에서 쉽게 볼 수 있는 항목을 말한다.
구체적으로는 Markowitz Model, CML, Asset Pricing Theory의 CAPM, Fama-French 3 Factor model, 그리고 APT까지를 다룬다. Sharpe ratio와 Infomration ratio도 추가했다.
전체적으로 영문 Wikipedia에 그림과 설명이 잘 나와있어서 번역한다.
Markowitz Model
Harry Markowitz가 1950년대에 만든 포트폴리오 최적화 이론이다.
마르코비츠는 다음의 가정 하에서 이론을 전개했다.
Assumptions 가정들
1. 포트폴리오의 risk 위험은 return 수익률의 varaiability에 기초한다.
2. An inverstor 투자자는 risk averse 위험 회피 성향이다.
3. 투자자는 comsumption 소비의 증가는 prefer 선호한다.
4. 투자자의 utility function 효용 함수는 concave이며 increasing이다. 왜냐면 위험회피와 소비 선호이기 때문에.
5. Analysis 분석은 투자의 single period 단일 기간에 기반한다.
6. 투자자는 포트폴리오의 주어진 레벨의 위험 하에서 수익률을 최대화하거나, 주어진 수익률에 대해서 위험을 최소화한다.
7. 투자자는 합리적이다.
굉장히 경제학적인 가정들이다.
여러가지 가능한 포트폴리오 중에서 가장 좋은 것을 고르기 위해서는 아래의 2가지 의사결정을 해야한다.
1. Efficient portfolios의 집합 결정
2. Efficient set에서 최상의 포트폴리오 선택
Determining the Efficient Set

점 T, S를 비교해보자. 투자자는 같은 위험인 $x_2$을 가졌지만 수익률은 S가 T보다 크다.
따라서 투자자는 T가 아니라 S를 선택하게 된다.
따라서 최선의 포트폴리오들의 점인 P, Q, S, V, W를 모두 연결한 선을 Efficient Frontier라고 한다.
Choosing the Best Portfolio
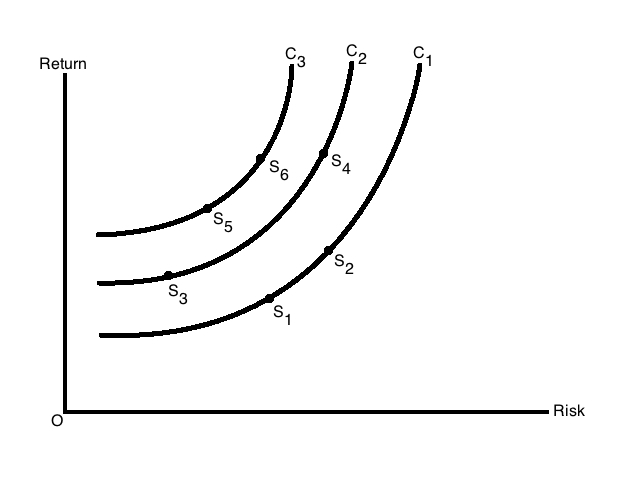
소비자의 효용함수는 Figure 2에 있는 indifference cureves 무차별 곡선이다. 효용의 경우 C1 곡선 보다 C2 곡선이 더 크다.
마찬가지로 C2 곡선 보다 C3 곡선이 더 크다.
C1 곡선 위의 $S1, S2$에서 투자자의 선호도에는 차이가 없다.

이제 위 무차별 곡선과 Efficient frontier를 함께 활용한다.
가장 큰 무차별 곡선을 선택하는게 좋으므로 C3과 frontier가 접하는 점을 찾는다.
지금까지는 주식 같은 risky securities 위험 자산에 대해서만 최적화를 수행했는데 아래에서는 risk-free securities 무위험 자산도 같이 고려한다.

R1을 무위험 수익률, 가령 정부의 채권 수익률이라고 한다. R1 부터 frontier에 이르는 접선을 그리고 이를 점 X까지 연장한다.
이 선을 Capital Market Line (CML)이라고 한다.
CML 직선은 capital market 자본 시장에서의 risk-return trade off 위험-수익의 트레이드 오프를 나타낸다.
P가 most efficient portfolio이고 모든 투자자들이 이를 선택한다면 이를 Market Portfolio라고 한다.
마켓 포트폴리오는 보통 most diversified 가장 다각화된 포트폴리오다.
마켓 포트폴리오에는 음의 수익률을 가진 자산과의 상관관계가 0이거나 상관관계가 1인 자산들을 포함하지 않는다.
CML 공식은 아래처럼 표기할 수 있다.
$R_P = I_{RF} + ( R_{M} - I_{RF} ) \sigma_{P} $ / $\sigma_{M}$
$R_P$ = 포트폴리오의 expected return 기대수익률
$I_{RF} $ = 무위험 자산의 rate of interest 이자율 (혹은 수익률)
$R_M$ = 마켓 포트폴리오의 수익률
$\sigma_{M} $ = 마켓 포트폴리오의 standard deviation 표준편차
$\sigma_{P} $ = 포트폴리오의 standard deviation 표준편차
$( R_{M} - I_{RF} ) $ / $\sigma_{M}$은 CML 곡선의 slope 기울기다.
$( R_{M} - I_{RF} ) $은 무위험 자산 대신 위험 자산에 투자하는 리스크 프리미엄을 측정한다.
$\sigma_{M} $은 마켓 포트폴리오의 위험을 나타낸다.
둘을 종합하면 기울기는 단위 위험에 대한 reward 보상를 뜻한다.
Asset Pricing Theory
자산의 가격을 결정하는 이론이다.
Capital Asset Pricing Model (CAPM)
Arbitrage Pricing Theory (APT)
등을 포함한다.
Capital Asset Pricing Model (CAPM)
E($R_i$) = $R_f$ + $\beta_i$ (E($R_m$ - $R_f$) )
- $R_f$는 무위험 자산의 이자율이다.
- $i$는 개별 capital asset이고 그에 대한 기대 수익률은 E($R_i$)다.
- 마켓의 기대 수익률은 E($R_m$)다.
- E($R_i$) - $R_f$ 는 individual risk premium 개별 위험 프리미엄이다.
- $\beta_i$는 자산 $i$이 market 시장에 대한 추가 수익률에 대한 sensitivity 민감도다.
Cov($R_i$, $R_m$) / Var($R_m$) 으로 정의한다. - 마켓의 기대 수익률은 E($R_m$)다.
- E($R_m$) - $R_f$ 는 market premium 시장 프리미엄이다.
- $\rho_{i, m}$은 자산 $i$와 시장 $m$ 사이의 corrleation coefficient다.
- $\sigma_i$는 자산 $i$에 대한 standard deviation이다.
- $\sigma_m$는 시장 $m$에 대한 standard deviation이다.
위 식을 다시 정리하면 아래와 같이 표현할 수 있다.
E($R_i$) - $R_f$ = $\beta_i$ (E($R_m$ - $R_f$) )
Fama-French 3 Factor model
CAPM에 2가지 factor 팩터를 추가한 확장 모델이다.
r = $R_f$ + $\beta (R_m - R_f) + b_s \cdot SMB + b_v \cdot HML + \alpha$.
SMB은 Small [market capitalization] Minus Big이고,
HML은 High [book-to-market ratio] Minus Low를 의미한다.
SMB는 소기업의 초과 수익률 - 대기업의 초과 수익률로 계산한다.
HML은 Book Value / Market Value = 장부가치 / 시장가치로 계산한다.
Book Value / Market Value은 PBR (Price-to-Book Ratio)의 역수로,
B/P가 높은 포트폴리오의 수익률 - B/P가 낮은 포트폴리오의 수익률로 계산한다.
Arbitrage Pricing Theory (APT)
E($R_i$) = $R_f$ + $ \sum_{j = 1}^{k} \beta_{i, j} \lambda_j $
무위험 자산과 여러개의 팩터의 선형결합으로 자산 $i$에 대한 수익률을 계산할 수 있다는 이론이다.
이때 $\lambda_j$는 개별 팩터이고 $\beta_{i, j}$는 자산 $i$에 대해서 팩터 $j$가 미치는 영향, factor loading이다.
거시경제적인 GDP, 이자율 등등을 사용할 수도 있다.
Fama-French가 APT의 특수한 경우라고 볼 수 있다.
기본적으로 multiple linear regression 다중 선형 회귀로 풀면 된다.
Sharpe Ratio and Information Ratio
Sharpe Ratio
샤프 레시오, 샤프 비율은 비교 대상이 되는 자산, benchmark 벤치마크 $b$에 대해서 자산 $a$의 초과 수익률과 위험을 계산한 비율이다.
여기서 벤치마크의 대상 자산은 risk-free asset이다.
Sharpe ratio는 다음과 같이 계산된다.
$S_a = \frac{ E \left[ R_a - R_b \right] }{ \sigma_a } = \frac{ E \left[ R_a - R_b \right] }{ \sqrt{V \left[ R_a - R_b \right] } } $
Information Ratio
인포메이션 레시오는 샤프 레시오의 일반화된 버젼으로, 벤치마크 자산이 risk-free asset이 아닌 다른 위험자산이 될 수 있다.
예시로 보면 삼성전자가 투자 고려 대상 위험 자산 $a$, 벤치마크 $b$가 KOSPI로 잡고 위와 동일한 식을 계산하면 된다.
References:
https://en.wikipedia.org/wiki/Modern_portfolio_theory
https://www.investopedia.com/terms/m/modernportfoliotheory.asp
https://en.wikipedia.org/wiki/Markowitz_model
https://en.wikipedia.org/wiki/Capital_market_line
https://en.wikipedia.org/wiki/Fama%E2%80%93French_three-factor_model
https://www.investopedia.com/terms/f/famaandfrenchthreefactormodel.asp
https://www.investopedia.com/terms/a/apt.asp
https://sec-api.io/resources/fama-french-factor-model
https://en.wikipedia.org/wiki/Sharpe_ratio
https://en.wikipedia.org/wiki/Information_ratio
https://www.schwab.com/learn/story/hows-that-fund-doing-check-information-ratio
'Time Series > Finance' 카테고리의 다른 글
| BloombergGPT (2023) 논문 리뷰 (0) | 2025.05.02 |
|---|---|
| SEC Fillings를 읽기 위한 회계용어 몇가지 정리 (1) | 2025.05.02 |
| SEC 미국 공시 관련 정보 모음 (0) | 2025.05.02 |
| Finance and Investment Introduction (2) | 2025.04.24 |
| Finance Data and LMs for NLP (0) | 2025.01.15 |

