Inception V3 (2015) 논문 리뷰

Inception V3 모델의 논문 제목은 Rethinking the Inception Architecture for Computer Vision이다. (링크)

 

저자는 Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, Zbigniew Wojna다.

 

 

 

Abstract

모델의 크기를 키우면서 적절히 factorized 분해된 컨볼루션들과 적극적인 regularization으로 효율적인 방법을 모색한 논문이다. 

ILSVRC 2012 분류 문제에서 SOTA를 달성하면서 동시에 25 million 이하의 파라미터 수를 유지했다.

 

3. Factorizing Convolutions with Large Filter Size

다른 블로그 글 (링크)를 보니 건너 뛴 Inception V2에서 상당 부분 연구된 부분을 좀 더 최적화한 논문이 Inception V3라고 한다.

 

기존의 5 x 5이나 7 x 7 같은 상대적으로 큰 filter size를 지니는 컨볼루션 연산의 연산량을 감소를 목표로 한다.

 

 

 

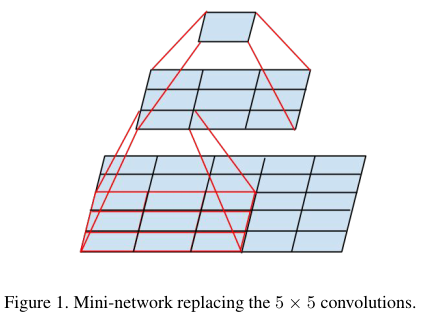
5 x 5 conv를 3 x 3을 2개로 대체해서 연산량을 줄이면서도 최종적인 receptive filed의 크기는 동일하게 만든다.

 

 

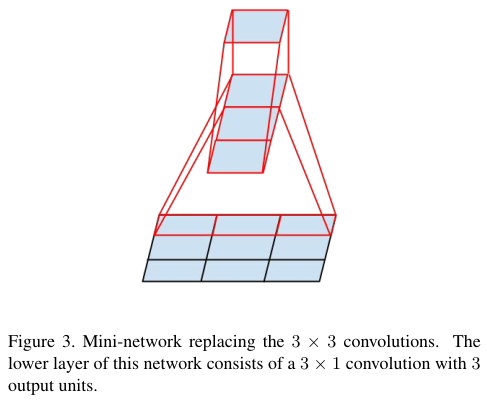
여기에다가 3 x 1 이나 1 x 3 같은 비대칭적인 컨볼루션도 도입한다.

 

 

Figure 4에 나온 구조가 원래의 Inception V1 모델에서 제시한 구조다.

 

 

 

 

 

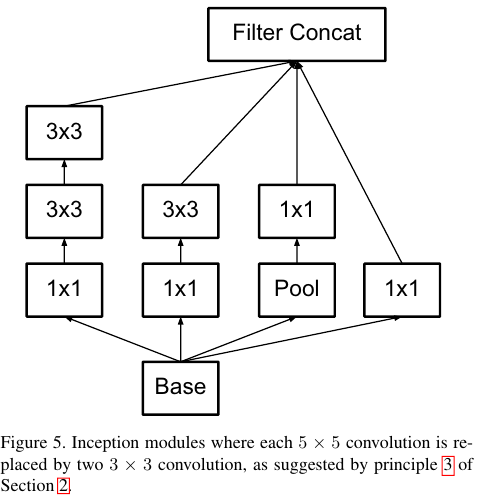
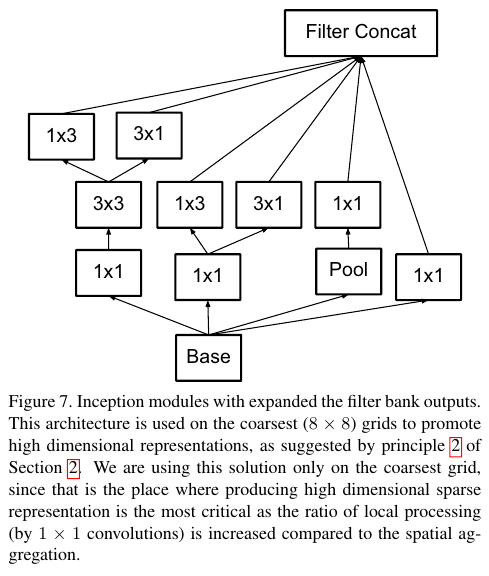
Figure 4를 5, 6, 8과 같이 계속해서 더 작은 컨볼루션들의 factorization으로 대체해서 효율화를 달성한다.

 

간단한 예시를 들면 5 x 5 컨볼루션의 경우 2개의 3 x 3 컨볼루션으로 대체하게 되면, 파라미터 수를 5 x 5 = 25에서 3 x 3 x 2 = 18로 줄일 수 있다. 

7 x 7 컨볼루션의 경우에는 3개의 3 x 3 컨볼루션을 사용하게 되므로, 7 x 7 = 49에서 3 x 3 x 3 = 27로 거의 절반이 된다. 

 

 

 

 

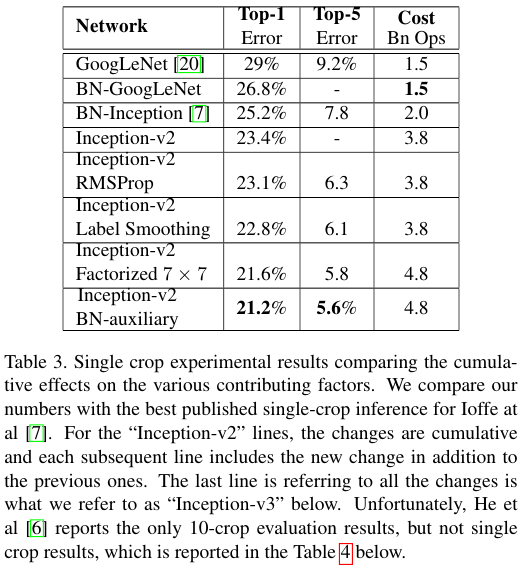
그리고 Table 3에서 본 것과 같이 RMSprop 옵티마이저 적용, Label smoothing, BN-auxiliary을 적용한다.

 

Label smoothing의 경우 모든 라벨 $k$에 대해서 아주 작은 값 $\epsilon$을 더해준다. 

 

원래의 라벨에 대한 예측값이 $\sigma_{k, y}$라면 라벨의 개수가 $K$ 일 때,

 

라벨에 대한 예측값은 $(1 - \epsilon)\sigma_{k, y} + \frac{\epsilon}{K}$이 된다.  

 

이 값을 이용해서 cross entropy를 구하고 이를 최종 loss로 사용하게 된다.

 

 

BN-auxiliary는 논문에 4. Auxiliary classifier라고 표기된 부분에 나온다. 

 

 

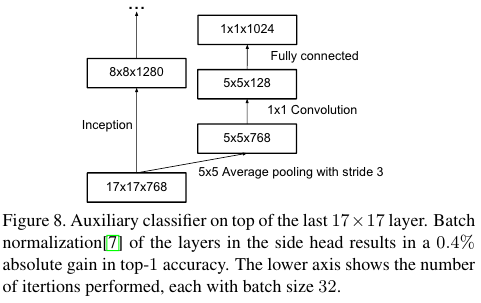
Auxiliary branch가 학습의 후반부에는 성능을 올린다는 연구가 있다.

BN-auxiliary의 뜻은 Auxiliary classifier의 fully connected layers가 batch normalized 되었다는 뜻이다.

 

 

 

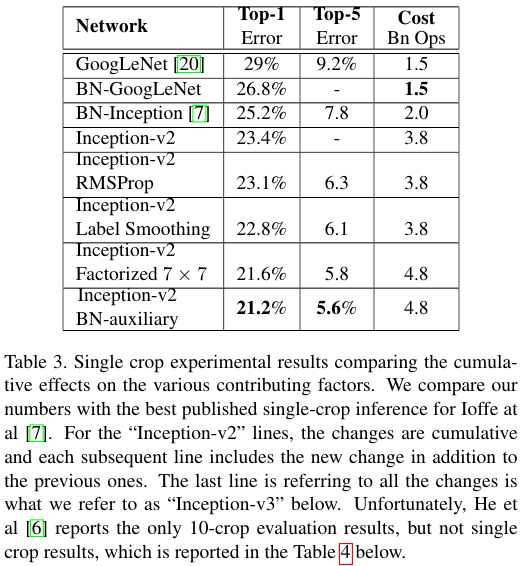
Table 3의 설명에도 나와있지만 Inception-v2를 시작으로 RMSProp, Label Smoothing, Factorized 7 x 7, BN-auxiliary를 아래로 누적하면서 하나씩 추가하면서의 성능을 보여준다.

 

Top-1과 Top-5의 에러가 감소함을 알 수 있다.

 

 

 

 

 

 

References:

https://hyunsooworld.tistory.com/entry/Inception-v1v2v3v4%EB%8A%94-%EB%AC%B4%EC%97%87%EC%9D%B4-%EB%8B%A4%EB%A5%B8%EA%B0%80-CNN%EC%9D%98-%EC%97%AD%EC%82%AC#2._Inception_V2,_V3