Kolmogorov-Arnold Networks는 원래의 초기 논문과 2.0의 2가지 논문이 있다.
여기서는 첫 번째 논문인 KAN: Kolmogorov-Arnold Networks (링크)을 중심으로 하고, 2.0은 간략하게만 다룬다.
KAN 오리지널 논문의 저자는 Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark다.
KAN 2.0의 논문 제목은 KAN 2.0: Kolmogorov-Arnold Networks Meet Science (링크)이고, 저자는 Ziming Liu, Pingchuan Ma, Yixuan Wang, Wojciech Matusik, Max Tegmark다.
Github: 링크
KAN은 Kolmogov-Arnold Theorem에 기반한 논문이다.
Kolmogorov-Arnold Theorem
Kolmogorov-Arnold Theorem은 multivariate continuous function $f$를 single variable functions의 finite composition으로 표현할 수 있다는 이론이다.
이때 $f: [0, 1]^n \rightarrow \mathbb{R} $
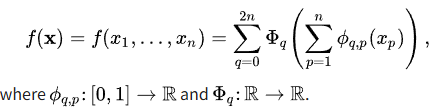
이를 통해서 고차원의 함수를 1차원의 함수의 합으로 표현할 수 있기에 분석하기 더 쉬워진다.
따라서 curse of dimensionality 차원의 저주를 피할 수 있다.
2. Kolmogorov-Arnold Networks (KAN)
저자들은 KAN을 이용해서 MLP를 대체하고자 한다.
MLP는 activation function이 고정되어 있고, affine transformation 뒤에 따라 오지만,
KAN은 반대로 function basis의 측면에서 작동하기 때문에 개별 노드들이 별개의 activation function을 갖는 효과가 있다.
아래 Figure 0.1.에 그림으로 MLP와 KAN의 차이가 나타나있다.
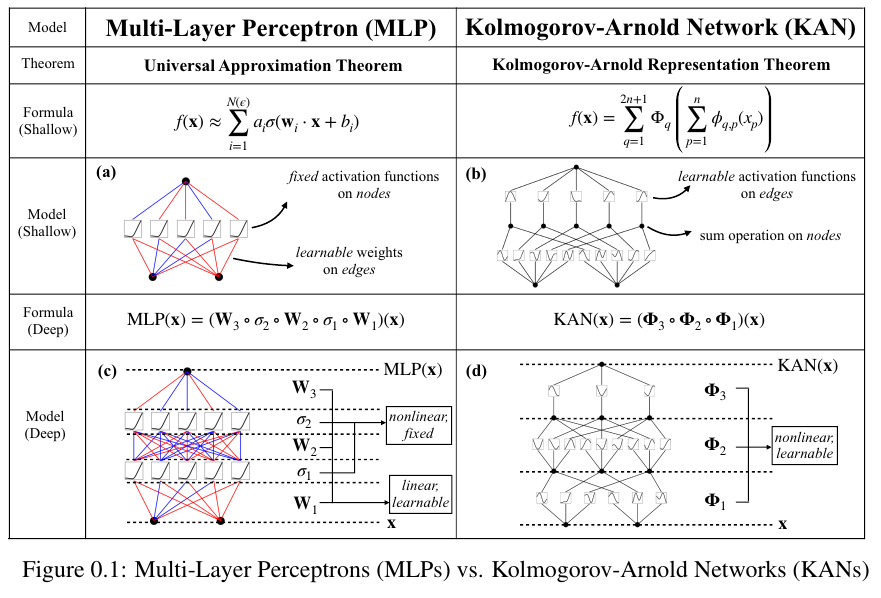
아래 Figure 2.1.에서는 KAN 논문의 전체적인 개요를 보여준다.
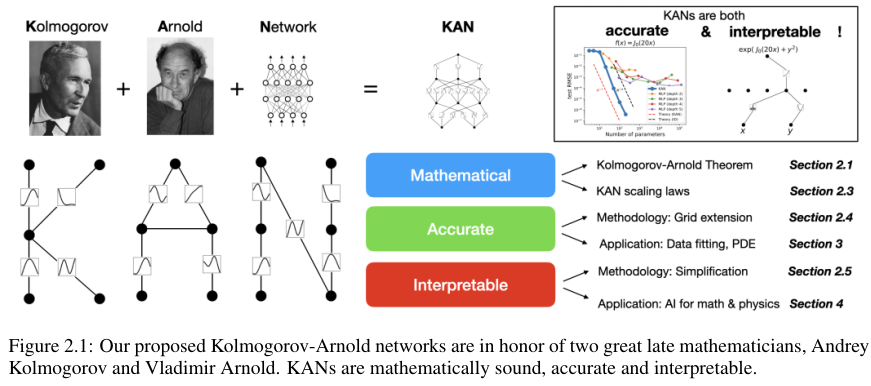
KAN layer는 $n_{in}$-dim inputs와 $n_{out}$-dim outputs에 대해서 다음의 1D functions의 행렬로 정의한다.
$\Phi$ = { $\phi_{q, p}$ } where $p$ = 1, 2, ..., $n_{in}$, and $q$ = 1, 2, ..., $n_{out}$
Kolmogorov-Arnold theorem에 의하면 inner functions 내부의 함수에서 $n_{in}$ = $n$이고, $n_{out}$ = 2$n$ + 1이다.
Outer functions에서는 반대로 $n_{in}$ = 2$n$ + 1이고, $n_{out}$ = $n$다.
Activation을 취하기 전 변수를 $x_{l, i}$로 표기한다.
레이어 $l$의 $i$번째 뉴런 = $(l, i)$-뉴런인 $x_{l, i}$와 레이어 $l+1$의 $(l + 1, j)$뉴런을 연결하는 $activation은 $\phi_{l, j, i}$로 표기한다.
Activation을 취한 결과는 $\tilde{x_{l, j, i}}$ = $\phi_{l, j, i} (x_{l, i})$로 표기한다.
$(l + 1, j)$ 뉴런은 다음의 equation (2.5)와 같이 post-activations의 합으로 표현이 가능하다.
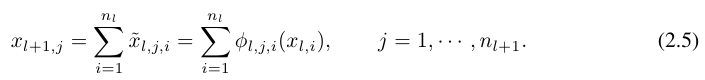
위 과정을 matrix form 행렬 형태로 나타내면 equation (2.6)과 같다.
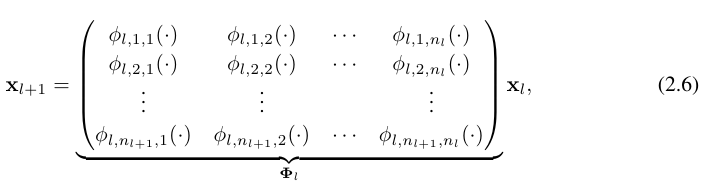
$\Phi_l$을 $l$th KAN 레이어에 해당하는 function matrix라고 하면,
$L$개의 레이어를 가진 general KAN network는 다음과 같이 표시할 수 있다.
KAN($\textbf{x}$) = $(\Phi_{L-1} \circ \Phi_{L-2} \circ ... \circ \Phi_{1} \circ \Phi_{0} ) \textbf{x}$
이는 곧 다음 (2.8) 처럼 표시할 수 있다.
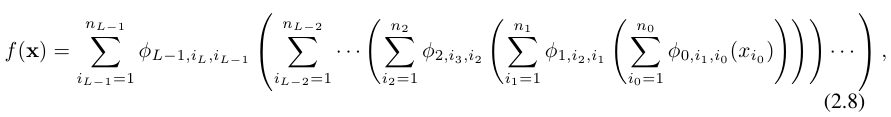
비교를 위해서 표기하면 MLP는 다음과 같이 표기할 수 있다.
$W$는 affine transformation이고 $\sigma$는 non-linear를 생성하는 함수다.
MLP($\textbf{x}$) = $(W_{L-1} \circ \sigma \circ W_{L-2} \circ \sigma \circ ... \circ W_{1} \circ \sigma \circ W_{0} ) \textbf{x}$
Implementation details
우선 basis function이라는 말이 나와서 간략하게 설명한다.
선형대수에서 vector space를 basis vectors들의 linear combination으로 구성할 수 있음은 널리 알려져있다.
이와 유사하게 function space를 basis functions들의 linear combination으로 구성할 수 있는 함수들이 basis function이고 한다.
앞에서 설정한 activiation function $\phi(x)$를 다음과 같이 정의한다.
$\phi(x) = w_b b(x) + w_s$ spline($x$).
이때 $b(x)$ = silu$(x)$ = $x$ / (1 + $e^{-x}$)다.
spline($x$) = $ \sum_i c_i B_i (x) $.
이때 $c_i$는 trainable 파라미터다.
Grid Extension
보다 정확하게 target function을 근사하기 위해서 spline을 더 잘게 쪼개서 더한다.
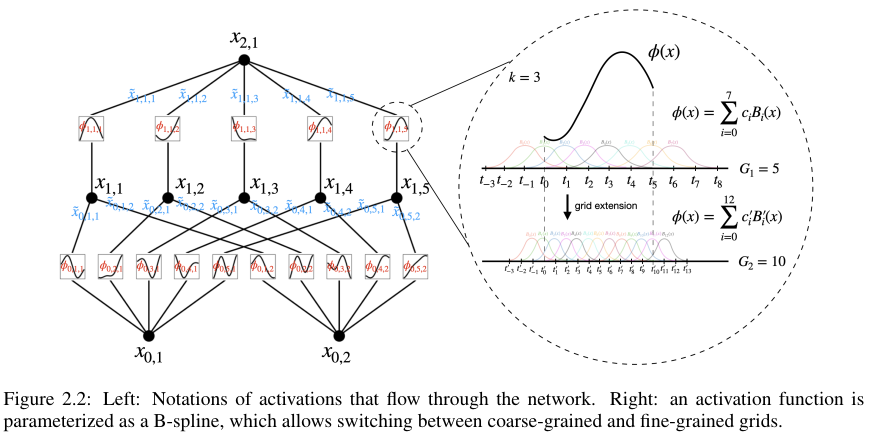
이는 정확도를 향상시키지만 computation은 증가하게 된다.
3. KANs are accurate
저자들은 KAN을 활용해서 수학적인 계산, symbolic function의 근사를 수행한다.

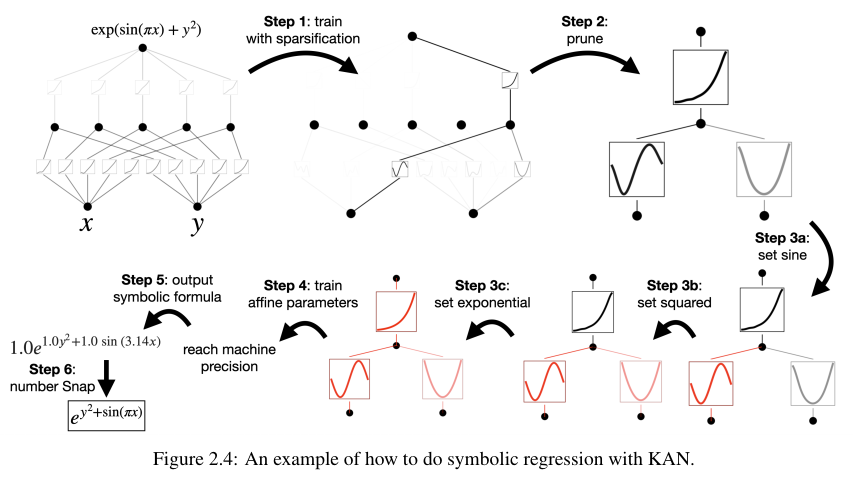
그리고 위 Figure 2.4를 보면 알겠지만 중간중간 필요없는 가지를 pruning해서 추론시의 파라미터 수를 줄인다.
Efficiency Comparison
Then there are in total O($N^2$ $L$(G + k)) ∼ O($N^2 L$G) parameters. In contrast, an MLP with depth $L$ and width $N$ only needs O($N^2 L$) parameters, which appears to be more efficient than KAN. Fortunately, KANs usually require much smaller $N$ than MLPs, which not only saves parameters, but also achieves better generalization
원문을 보면 Big O 표기법으로 원래 KAN이 MLP보다 비효율적이지만, 대체로 같은 성능에 대해서 KAN이 더 작은 $N$을 요구하기 때문에 더 효율적이라고 하고 있다.
마지막으로 저자들이 생각하는 MLP와 KAN의 비교는 아래 Figure 6.1에 나와있다.
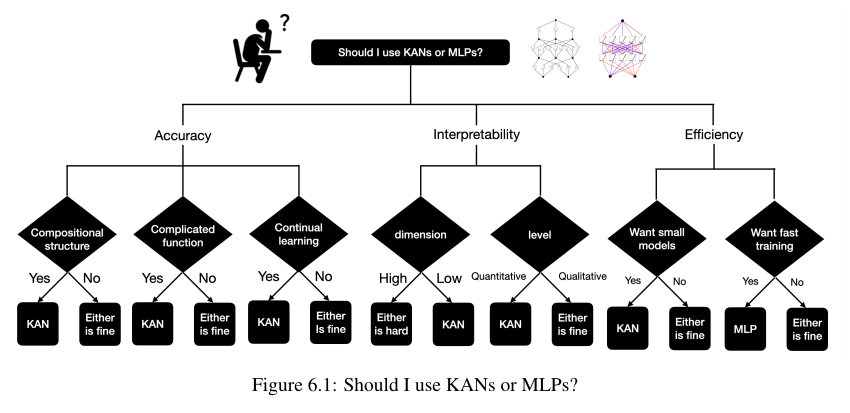
여기까지는 KAN 오리지널 논문의 내용이다.
KAN 2.0 MultKAN
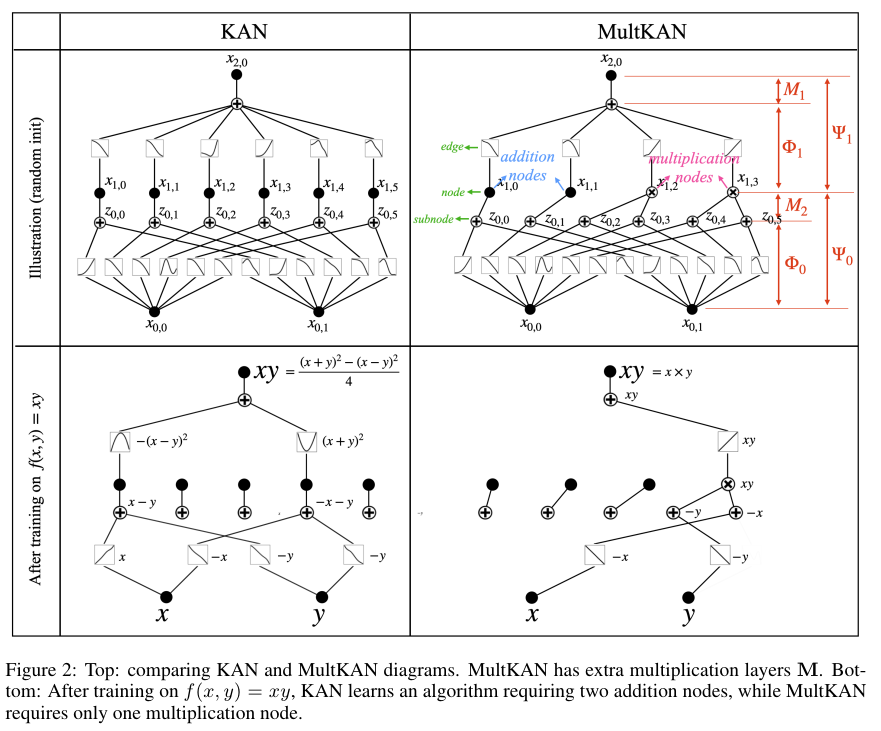
KAN 2.0은 위 Figure 2에 나와있듯이 Addition 뿐만 아니라 Multiplication을 추가한 방법론이다.
이를 통해서 아래 Figure 5에서처럼 과학 계산에 있어서 더 유연하게 확장이 가능하다고 한다.
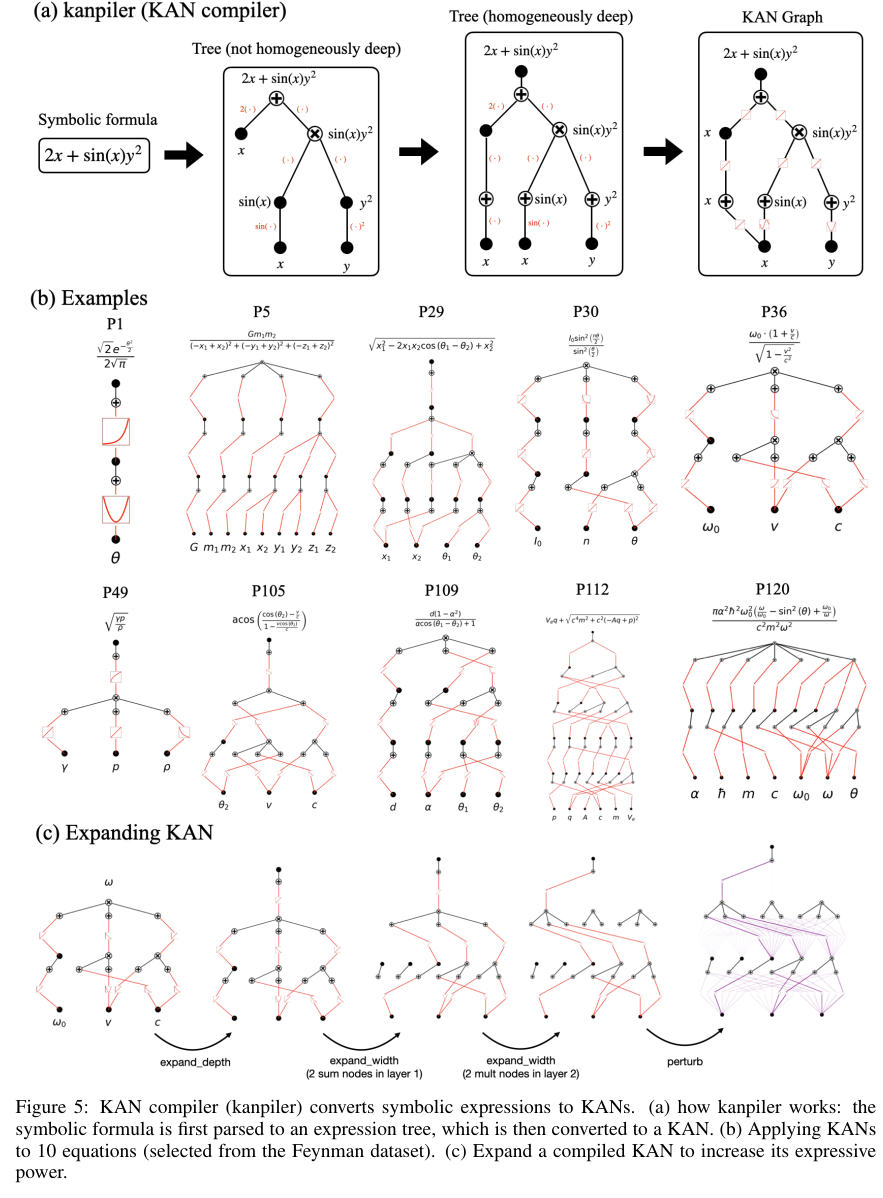
추가로 논문에서 model.speed를 통해서 모델의 fit에 있어서 속도를 증가시킬 수 있다고 나와있다.
이는 구현된 코드 (링크)에 보면 speed 함수는 아래와 같음을 확인할 수 있다.
def speed(self, compile=False):
'''
turn on KAN's speed mode
'''
self.symbolic_enabled=False
self.save_act=False
self.auto_save=False
if compile == True:
return torch.compile(self)
else:
return self
symbolic_enabled와 save_act, 그리고 auto_save가 중간에 속도를 저하시키는 요소임을 확인할 수 있다.
References:
https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Arnold_representation_theorem
https://brunch.co.kr/@leadbreak/24
https://en.wikipedia.org/wiki/B-spline
https://en.wikipedia.org/wiki/Basis_function
'Deep Learning' 카테고리의 다른 글
| ODIN (2018) 논문 리뷰 (2) | 2025.07.25 |
|---|---|
| Quantization 정리 (0) | 2025.05.20 |
| Floating-point Number와 Mixed Precision (0) | 2025.04.29 |
| Meta, Few-shot, Zero-shot, Active Learning (0) | 2024.10.25 |
| 딥러닝 모델 분석과 구현 정리 (0) | 2024.04.24 |


