우선 그래프를 다음 2가지를 활용해서 (링크1, 링크2)에 간략하게 살펴보자면 다음과 같다.
결국, 무언가들의 연결을 알아보기에 좋은 자료 형태다.
추천의 경우 이 사람이 이 영화를 좋아하는 이유가 영화의 장르 때문인지, 배우 때문인지 등을 연결 관계에 대해서 살펴보면 확인할 수 있다.
SNS나 바이러스의 확산 같은 경로의 전파에도 쓸 수 있다. 추천의 경우 어떤 집단에서 다른 집단으로 퍼져나가는지를 확인할 수도 있을 것 같다.
Basic Graph Neural Networks
Adjacency matrix 인접 행렬이나 이를 이용해서 도출하는 Laplacian Matrix를 MLP들을 통해서 학습하는 기본적인 형태의 Graph Convolutional Network를 생각할 수 있다.
GNNs in Recommendation
GNN을 통해서 그래프와 관련된 여러가지 작업을 수행할 수 있다.
노드 수준에서 해당 노드의 성격을 정의하거나 발굴하여, 즉 노드 = 유저가 어떤 특성을 지닌 사람인지 구분할 수 있다.
반면에 엣지 = 링크 수준에서, 두 노드 사이의 관계를 예측하는 작업을 수행할 수 있다. 이 경우 어떤 아이템을 추천할지에 사용할 수 있다.
여기서는 다음의 유명한 모델들만을 살펴본다.
- PinSAGE
- NGCF
- KGCN
- LightGCN
- KGAT
PinSAGE
논문 제목은 Graph Convolutional Neural Networks for Web-Scale Recommender Systems (링크)다.
PinSAGE는 Pinterest에서 발표한 논문으로 GraphSAGE 모델 (Inductive Representation Learning on Large Graphs, 링크)에서 많은 부분을 참고하였다.
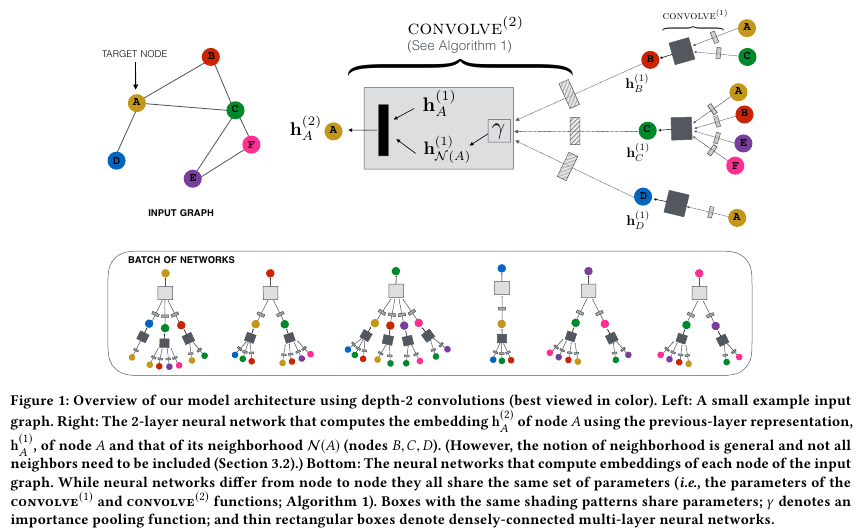
PinSAGE에서는 bipartite graph를 이용한다. 서로 disjoint인 두 개의 집한 사이에서만 직접적인 link를 생성한다. 여기서는 pins의 집합인 $I$와 boards의 집합인 $C$다. 보통은 user set와 item set인데 핀터레스트에서는 그게 아니라 pin와 board 사이의 관계를 정의한다는 점이 특이하다.
그리고 Adjacency matrix를 학습하는게 아니라 다른 방식으로 node의 neighbor nodes의 정보를 학습한다.
Forward propogation algorithm

GraphSAGE처럼 PinSAGE 역시 주어진 노드 $u$의 neighbors 이웃 노드들을 aggragate한다. $\gamma$로 표현되는 Aggragate 함수는 element-wise mean이나 element-wise weughted sum이다.
Importance-based neighborboods
이때 모든 k-hop의 노드들을 사용하는게 아니라 Pixie: A System for Recommending 3+ Billion Items to 200+ Million Users in Real-Time.논문에서 제시한 바와 같이 Random walk를 통해서 얻은 noralized visit counts가 가장 큰 top $T$개의 노드만을 사용한다. (k-hop이란, 연결된 링크의 수가 k인 이웃 노드를 의미한다. 예를 들어서 a - b, b - c, c - d로 연결되어있다면 a와 b는 1-hop, a와 b는 2-hop, a와 d는 3-hop이다.)

위 Algorithm 2에서 제시된 바와 같이 미니 배치 단위로 학습한다.
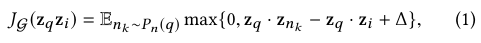
이때 위와 같은 Max margin based loss가 목적함수다. 이때 주어진 노드에 대한 negative samples가 필요한데, 전체 2 B개의 아이템들 중에서 500개만 뽑아서 사용한다. 대신 학습을 용이하게 하기 위해서 잘 구분하지 못하는 Hard negatives를 사용한다.
NGCF
NGCF의 논문 제목은 Neural Graph Collaborative Filtering (링크)다.
NGCF는 l-hop의 이웃 노드들의 연결을 embedding propogation layers로 학습하는 모델이다.
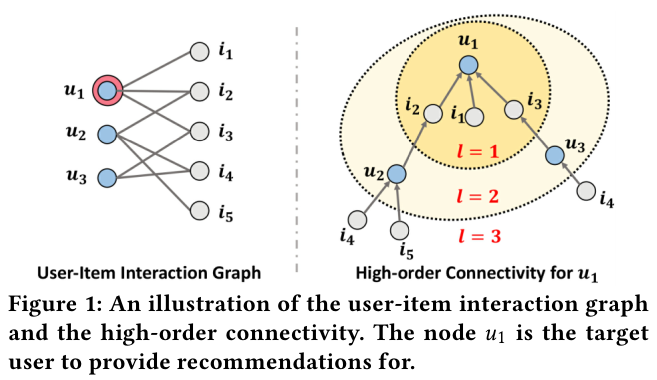
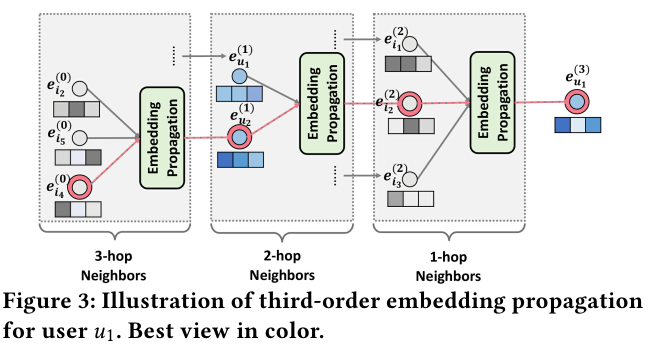
위 Figure 1과 3에서 제시되었듯이, 주어진 노드 $u_1$에 연결된 multi-hop의 이웃 노드들을 embedidng layers를 통해서 학습하여 전파한다. 가장 먼 이웃 노드들에서 부터 가까운 노드로 정보를 전파한다.
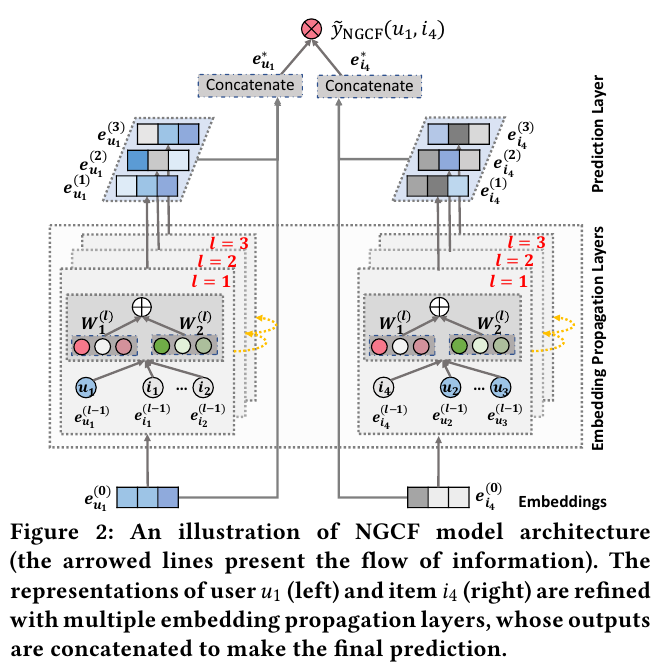
Multi-hop에서 학습한 각각의 hop의 정보들을 개별적으로 임베딩으로 만들고, concat해서 user 1에 대한 임베딩 $e_{u_1}^{*}$ 그리고 item 4에 대한 임베딩 $e_{i_4}^*$예측 값을 도출한다. 그리고 이 두 임베딩을 통해서 예측 값 $\hat{y}$를 도출한다.
KGCN
KGCN의 논문 이름은 Knowledge Graph Convolutional Networks for Recommender Systems (링크)다.
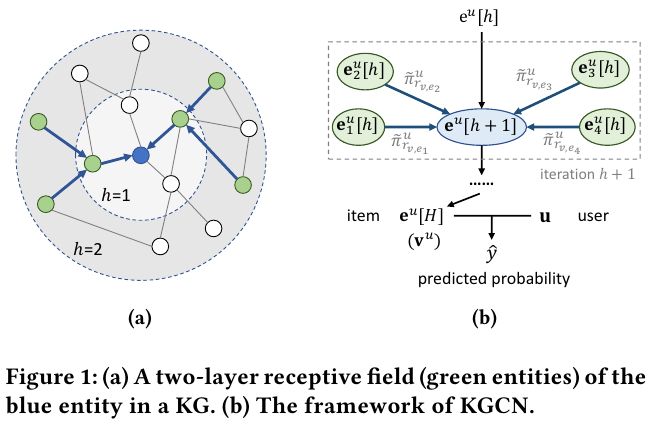
유저 $u$, 아이템 (entity) $v$, 그리고 두 entity 사이의 relation 관계는 $r_{e_i, e_j}$로 표기한다.
유저 $u$와 관계 $r$간의 score 점수는 $\pi_{r}^{u} = g(\text{u}, \text{r})$로 표기한다. 이때 $\text{u}, \text{r} \in \mathbb{R}^d$인 임베딩이고, $g: \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}$인 함수다.
유저 $u$와 아이템 $v$ 사이의 예측 점수는 다음와 같이 예측한다.
$\text{v}_{N(v)}^n = \sum_{e \in N(v)} \tilde{\pi}_{r_{v, e}}^{u} \text{e}$.
이때, $\tilde{\pi}_{r_{v, e}}^{u}$은 softmax의 형태로 normalized한 user-relation score다.
$\text{e}$는 entity $e$의 representation이다.
위와 같이 여러개의 relation을 더하는 이유는 유저 $u$와 아이템 $v$ 사이의 여러가지 관계를 사용할 수 있기 때문이다.
예를 들어서 영화의 경우 genre, actors, scores 등의 관계를 유저와 가질 수 있는데 이러한 내역들을 모두 반영하기 위해서다.
이게 바로 다양한 relation (link 혹은 edge)를 가지는 Knolwedge Graph를 활용의 특징이다.
KGCN의 aggergation은 Sum, Concat, Neighbor의 세 종류가 있다.

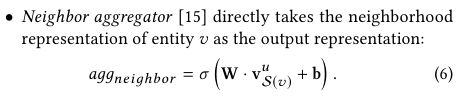
Sum, Concat, neighbor 연산을 한 다음에 Affine Transformation과 non linear activation을 적용해서 각각의 관계를 학습한다.
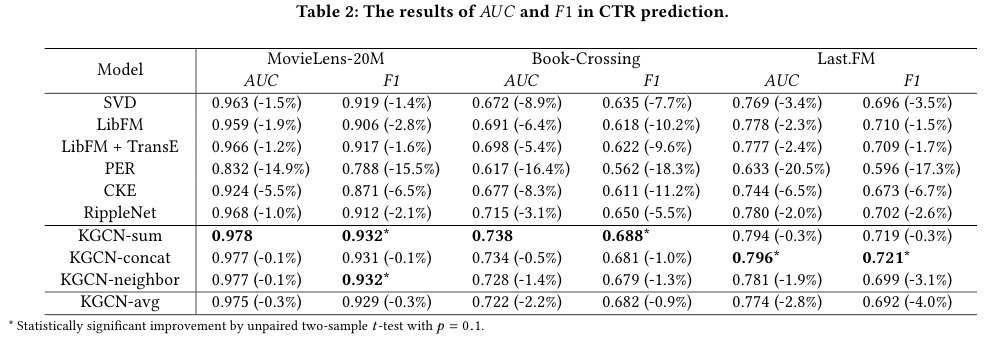
위 Table 2를 보면 알겠지만, 데이터에 따라서 최상의 aggregator이 다르다. 따라서 실험해보고 선택해야 한다. 하지만 일반적으로는 sum이 좋은 성능이라고 간주할 수도 있다.
LightGCN
LightGCN 논문의 제목은 LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation (링크)다.
아래 Figure 2를 보면 알 수 있듯이 NGCF의 aggregation을 단순화하여 더 빠르게 수렴하게 만든다.
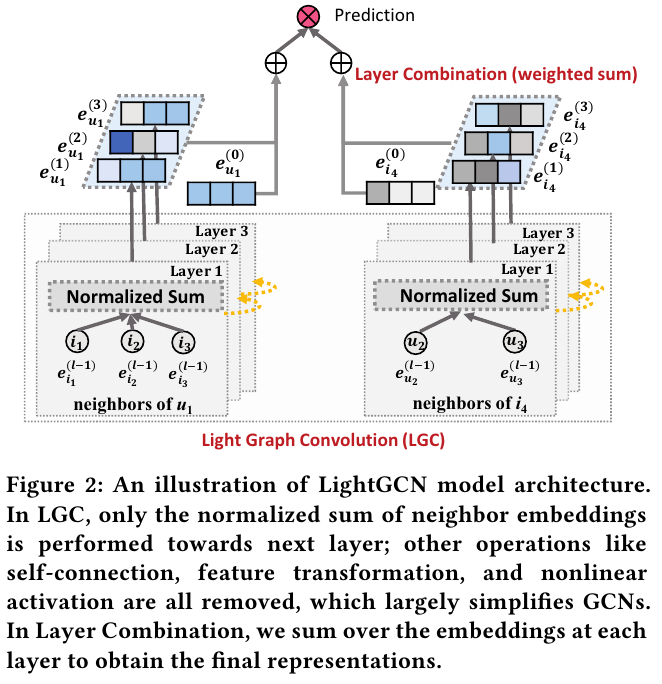
Affine transformation과 non-linear 연산 대신에 단순하게 neighbors의 임베딩을 더하고 scaling한다.
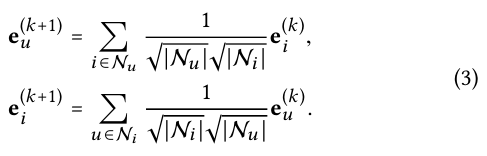
KGAT
KGAT의 논문 제목은 KGAT: Knowledge Graph Attention Network for Recommendation (링크)다.
기본적으로 KGAT는 제목에서 파악할 수 있듯이 Knowledge Graph을 활용한다. Figure 1에서처럼 다양한 relations을 활용한다.
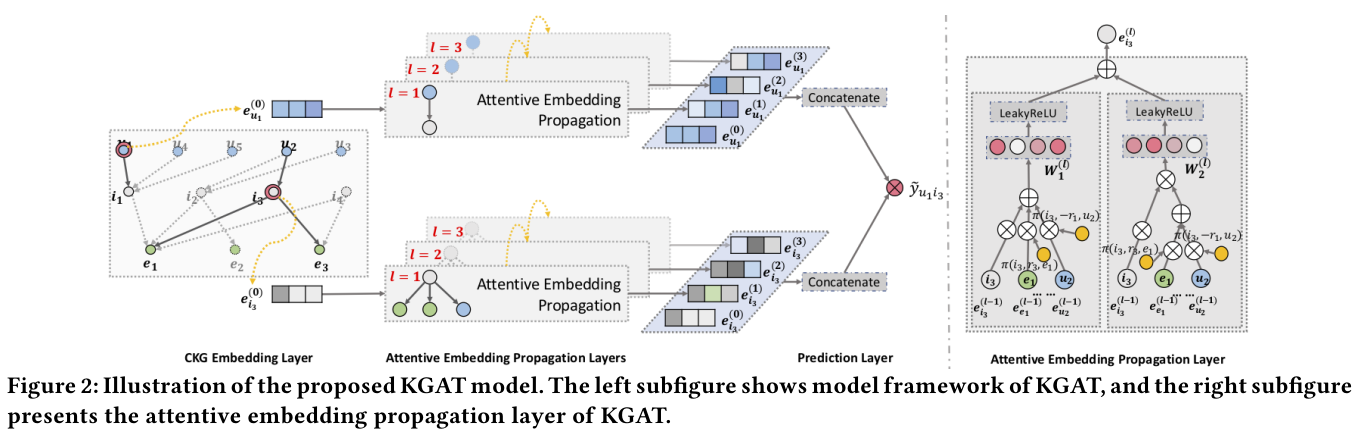
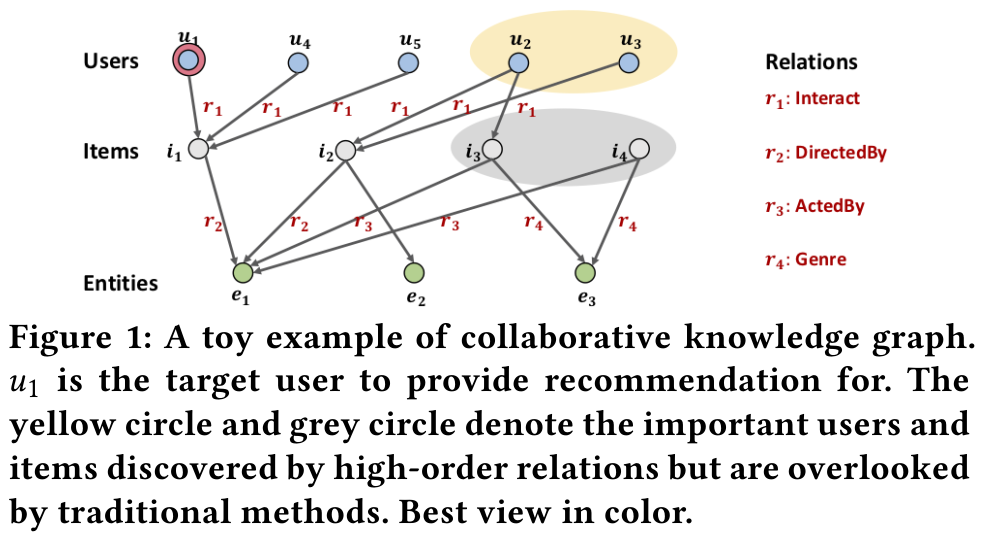
전반적인 KGAT의 모델 구조는 위 Figure 2에 나와있다.
2가지 그래프를 사용한다.
User-Item Bipartite Graph $\mathcal{G}_1 = \{ (u, y_{ui}, i | u \in \mathcal{U}, i \in \mathcal{I}) \}$이고 $\mathcal{U}$은 user set, $\mathcal{I})$은 item set이다. 두 집합은 서로 disjoint다. 유저 $u$와 아이템 $i$ 사이의 interaction이 관측되면 $y_{ui}$을 1로, 상호작용이 없으면 0으로 설정한다.
Knowledge Graph는 아이템을 위한 side information을 담는 그래프다. 이는 item attributes나 external knowledges를 의미한다. 수식으로 표기하면 다음과 같다. $\mathcal{G}_2 = \{ (h, r, t) | h, t \in \mathcal{E}, r \in \mathcal{R}) \}$이다. 이는 subject-property-object의 triple로 구성된다. r은 relation이고, h는 head entity, t는 tail entity다. 예를 들어서 (Hugh Jackman, ActorOf, Logan)은 h가 배우 휴 잭맨, r은 ActorOf, t는 영화 로건임을 나타낸다. 추가적으로 Item-entity alignments 집합 $ \mathcal{A} = \{ (i, e) | i \in \mathcal{I}, e \in \mathcal{E} \} $을 이용해서 아이템 $i$가 entity $e$에 aligned 됨을 의미한다.
Given triplet $(h, r, t)$에 대한 plausibility score (or energy score)는 아래와 같이 표시한다. 이때, $W_r$은 relation $r$에 대한 transformation matrix다.
$ g(h, r, t) = || W_r e_h + e_r - W_r e_t ||_2^2 $
Pairwise ranking loss는 다음과 같이 정의한다.
$L_{KG} = \sum -ln \sigma( g(h, r, t') - g(h, r, t) )$
이때, $(h, r, t')$는 broken triplet으로 유효한 triplet에서 하나의 entity를 임의로 대체한 triplet이다.
Knowledge-aware Attention
Decay factor $\pi(h, r, t) = (W_r e_t)^\top$ tanh $( (W_r e_h + e_r ) )$로 정의한다.
그리고 위 $\pi(h, r, t) $은 집합 $N_h$, head entity $h$가 있는 모든 triplet을 사용하여 softmax로 normalize한다.
$h$에 대한 최종 first-order ego-network는 아래처럼 weighted sum으로 표기한다.
$e_{N_h} = \sum_{(h, r, t) \in N_h} \pi(h, r, t) e_{t} $
Information Aggregation
Entity represenation $e_h$와 h의 ego-network $e_{N_h} $의 합계 함수 $f$는 다음의 3가지 방식을 제시한다.
1. GCN Aggregator
Sum을 사용한다.
LeakyReLU($W(e_h + e_{N_h})$)
2. GraphSage Aggregator
Concatenation || 을 사용한다.
LeakyReLU($W(e_h || e_{N_h})$)
3. Bi-Interaction Aggregator
Element-wise product $\odot$을 사용한다.
LeakyReLU($W(e_h + e_{N_h})$) + LeakyReLU($W(e_h \odot e_{N_h})$)
High-order Propogation
$e_h^{(l)} = f( e_h^{(l - 1)}, e_{N_h}^{(l-1)} )$
$e_{N_h}^{(l-1)} = \sum_{(h, r, t) \in N_h} \pi(h, r, t) e_{t}^{(l - 1)} $
Model Prediction
모델의 최종 예측의 과정은 다음과 같다.
$e_u^* = e_u^{(0)} || ... || e_u^{(L)} $
$e_i^* = e_i^{(0)} || ... || e_i^{(L)} $
$\hat{(y)} (u, i) = {e_u^*}^{\top} e_i^* $
이 예측에 대한 loss function은 아래와 같이 정의한다.
$L_{CF} = \sum -ln \sigma( \hat(y) (u, i) - \hat(y) (u, j) )$
이때, $j$는 interaction이 없는 negative item이다.
$L_{CF} $와 $L_{KG}$ 그리고 파라미터의 L2 regularization을 합친 total loss를 최소화하여 모델을 최적화한다.
References:
https://medium.com/@rguoasu/graph-convolutional-neural-network-621bd88143ce
https://tkipf.github.io/graph-convolutional-networks/
https://www.ibm.com/think/topics/graph-neural-network
https://blogs.nvidia.com/blog/what-are-graph-neural-networks/
https://greeksharifa.github.io/machine_learning/2021/02/21/Pin-Sage/
https://www.ibm.com/kr-ko/think/topics/knowledge-graph
https://en.wikipedia.org/wiki/Knowledge_graph
'Recommender Systems' 카테고리의 다른 글
| Session-based & Sequential Recommender Systems (0) | 2025.06.20 |
|---|---|
| Socio Based Recommender Systems (0) | 2025.06.20 |
| Matrix Factorization Based Recommender Systems (1) | 2025.06.20 |
| 추천 시스템 라이브러리와 데이터 리서치 (3) | 2025.06.19 |
| Towards Next-Generation LLM-based Recommender Systems (2024) 논문 리뷰 (2) | 2025.05.16 |


