LoRA의 논문 이름은 LoRA: Low-Rank Adaptation of Large Language Models다. (링크)
저자는 Edward J. Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, Weizhu Chen다.
Github: 링크
이름에서 알 수 있듯이 기존의 adapter 레이어를 추가하는 방식과 같지만 이를 low-rank로 만든다는 점에서 차이가 있다.
여기서 말하는 rank는 선형대수의 그 rank가 맞다.
Abstract
GPT-3 175B와 같은 큰 모델의 파인 튜닝은 매우 비싸다. 따라서 저자들은 Low-Rank Adaptation, LoRA를 제시한다.
모델의 원래 weigths를 프리즈하고 trainable rank decomposition matrices를 추가하는 구조다.
RoBERTa, DeBERTa, GPT-2 그리고 GPT-3에 대해서 파인튜닝한 퀄리티를 비교한다.
다른 adapters와는 다르게 addtional inference latency 추가적인 추론 레이턴시가 없다.

2. Problem Statement
Full fine-tuning의 최적화 과정은 아래 식과 같다.
$ \underset{\Phi}{\operatorname{max}} \sum_{(x, y) \in Z } \sum_{t = 1}^{|y|} log( P_{\Phi} ( y_t | x, y_{<t}) )$
pre-trained weights $\Phi_0$을 $\Phi_0 + \Delta \Phi$로 업데이트 한다.
이때 $|\Delta \Phi_0|$ = $| \Phi_0|$ 이므로 많은 양의 파라미터를 업데이트 해야 한다.
하지만 LoRA 논문에서 제시한 parameter-efficient 방법의 파라미터 증가분 $\Delta \Phi_0$ = $\Delta \Phi (\Theta) $다.
이때 $\Theta$는 훨씬 작은 크기의 파라미터다. $|\Theta|$ << $|\Phi_0|$.
따라서 보다 파라미터-효율적인 최적화 식은 아래와 같다.
$ \underset{\Theta}{\operatorname{max}} \sum_{(x, y) \in Z } \sum_{t = 1}^{|y|} log( p_{\Phi_0 + \Delta \Phi(\Theta) } ( y_t | x, y_{<t}) ) $
GPT-3의 175 B인 $|\Phi_0|$와 비교할 때 $|\Theta|$는 $|\Phi_0|$의 0.01%에 불과한 작은 크기다.
4. Our Method
본래의 forward path인 $h = W_0 x$를 adapter layer를 적용한 modified forward path는 아래와 같다.
$h = W_0 x + \Delta W x = W_0 x + B A x$.
이때, Weight matrix $W_0 \in {\mathbb{R}}^{d \times k}, B \ in {\mathbb{R}}^{d \times r}, A \in {\mathbb{R}}^{r \times k} $ 이며, $r$ << min($d, k$)다.
$A$에 대해서는 random Gaussian initialization을 수행하고 $B$는 0으로 초기화 한다. 따라서 $\Delta W = BA$는 학습 초기에는 0이다.
5. Empirical Experiments
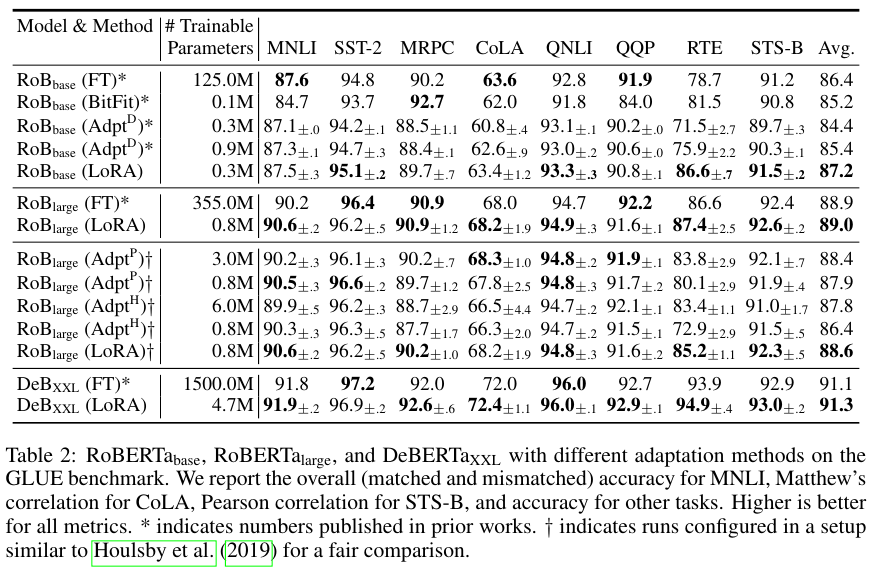


RoBERTa, DeBERTa, GPT-2, GPT-3에 대해서 다른 파인 튜닝 방법들과 비교한 결과 LoRA가 훨씬 적은 수의 파라미터로도 대체로 좋은 성능을 달성했음을 알 수 있다.


Table 5와 6은 Transformer 구조에서 어떤 레이어에 LoRA를 적용할 때 성능이 가장 좋은지, 그리고 low rank를 결정하는 $r$이 얼마나 작아야 하는지를 나타낸 표다.
$q, k, v, o$ 모두에 LoRA를 적용한다면 $r$이 무려 1이어도 좋은 성능을 달성함을 알 수 있다.
References:
https://asidefine.tistory.com/309
https://minyoungxi.tistory.com/116
https://pytorch.org/torchtune/0.4/tutorials/lora_finetune.html
https://github.com/huggingface/peft/blob/main/src/peft/tuners/lora/model.py
'NLP > LLM' 카테고리의 다른 글
| LaMDA (2022) 논문 리뷰 (0) | 2025.04.11 |
|---|---|
| Scaling Laws for Neural Language Models (2020) 논문 리뷰 (0) | 2025.04.11 |
| OPT (2022) 논문 리뷰 (0) | 2025.04.11 |
| GPT 3 (2020) 논문 리뷰 (0) | 2025.04.09 |
| Small Language Models: Survey, Measurements, and Insights (0) | 2025.03.17 |



